B

B

B

Đường thẳng d có VTPT  n d → ( 2 ;    − 3 )

Gọi đường thẳng ∆ thỏa mãn có VTPT   n Δ → ( a ;    b )

 Vì góc giữa hai đường thẳng bằng 60⁰ nên:

cos 60 0 = c os (  n d → ;     n Δ → ) = 2 a − 3 b 2 2 + ( − 3 ) 2 .   a 2 + ​ b 2 ⇔ 1 2 = 2 a − 3 b 13 .   a 2 + ​ b 2 ⇔ 13 .   a 2 + ​ b 2 =   2.    2 a − 3 b ⇔ 13 ( a 2 + ​ b 2 ) = 4 ( 4 a 2 − 12 a b + ​ 9 b 2 ) ⇔ − 3 a 2 + ​ 48 a b − 23 b 2 = 0 ⇔ − 3 a b 2 + ​ 48. a b − 23 = 0 ​​​      ( * )

Phương trình (*) có 2 nghiệm phân biệt. Ứng với mỗi nghiệm ta tìm được 1 cặp số (a, b) là VTPT của đường thẳng ∆. Từ đó, ta viết được 2 phương trình đường thẳng ∆ thỏa mãn. 

ĐÁP ÁN C

trl ; bạn kia đúng r

-

_

----------------

\(\Delta:2x+3y-1=0.\)

\(\Rightarrow\) VTPT của \(\Delta\) là \(\overrightarrow{n_{\left(\Delta\right)}}=\left(2;3\right).\)

Phương trình đường thẳng \(\left(d\right)\) song song với đường thẳng \(\Delta:2x+3y-1=0.\) 

\(\Rightarrow\) VTPT của đường thẳng \(\Delta\) cũng là VTPT của đường thẳng \(\left(d\right).\)

\(\Rightarrow\) VTPT của \(\left(d\right)\) là \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right).\)

Ta có đường thẳng \(\left(d\right)\) nhận \(\overrightarrow{n_{\left(d\right)}}=\left(2;3\right)\) làm VTPT; đi qua điểm \(A\left(3;-1\right).\)

\(\Rightarrow\) Phương trình đường thẳng \(\left(d\right)\) là:

\(2\left(x-3\right)+3\left(y+1\right)=0.\\ \Leftrightarrow2x-6+3y+3=0.\\ \Leftrightarrow2x+3y-3=0.\)

Đáp án C

+phương trình ∆ đi qua M (8; 2) và vuông góc với d  là:

3 (x-8) +2(y-2) =0 hay 3x+2y -28= 0.

+ Gọi  H = d ∩ ∆ ⇒ H ( 6 ; 5 )

+ Khi đó H là trung điểm của đoạn MM’. Áp dụng công thức trung điểm ta suy ra

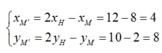
Vậy M’( 4;8) .

Lời giải:

VTPT của $(d)$: $(2,-3)$

Đường thẳng $\Delta$ vuông góc với $(d)$ nên VTCP của $(\Delta)$ chính là $(2,-3)$

$\Rightarrow$ VTPT $ của $(\Delta)$ là $(3,2)$

PTĐT $(\Delta)$: $3(x-1)+2(y-2)=0$

$\Leftrightarrow 3x+2y-7=0$

d nhận \(\left(2;3\right)\) là 1 vtpt nên nhận \(\overrightarrow{u}=\left(3;-2\right)\) là 1 vtcp

Do \(B\in d\) nên tọa độ có dạng: \(B\left(b;\dfrac{-2b-4}{3}\right)\Rightarrow\overrightarrow{AB}=\left(b-1;\dfrac{-2b-7}{3}\right)\)

\(cos45^0=\dfrac{\left|3.\left(b-1\right)+\dfrac{2\left(2b+7\right)}{3}\right|}{\sqrt{3^2+2^2}.\sqrt{\left(b-1\right)^2+\left(\dfrac{2b+7}{3}\right)^2}}=\dfrac{1}{\sqrt{2}}\)

\(\Leftrightarrow2\left(13b+5\right)^2=13\left(13b^2+10b+58\right)\)

\(\Leftrightarrow169b^2+130b-704=0\Rightarrow\left[{}\begin{matrix}b=-\dfrac{32}{13}\\b=\dfrac{22}{13}\Rightarrow y_B=-\dfrac{32}{13}< 0\left(loại\right)\end{matrix}\right.\)