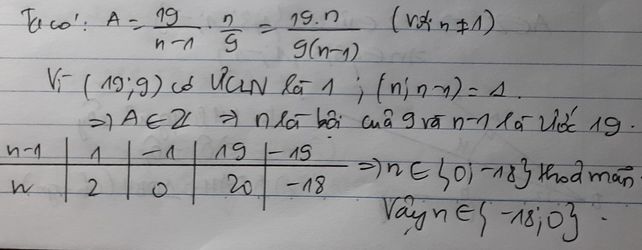Những câu hỏi liên quan
tìm n \(\in\) Z để tích hai phân số \(\frac{19}{n-1}\)(với n \(\ne\))và \(\frac{n}{9}\)có giá trị là số nguyên
=> cả 2 phân số phải là số nguyên
*19 chia hết cho (n-1)
| n - 1 | -1 | 1 | -19 | 19 |
| n | 0 | 2 | -18 | 20 |
*n chia hết cho 9 => n = 0 hoặc -18
Đúng 0
Bình luận (0)
Tìm n\(\in\) Z để tích hai phân số \(\dfrac{19}{n-1}\)với (n\(\ne1\)) và \(\dfrac{n}{9}\)có giá trị là số nguyên
Để tích 2 PS là số nguyên thì 19⋮n-1 và n⋮9
⇒n-1∈Ư(19),9∈B(n)
⇒Ư(19)={\(\pm\)1;\(\pm\)19}
⇒n-1=1 ⇒n-1=19
⇒n-1=-1 ⇒n-1=-19
⇒n∈{2;20;0;-18} nhưng 9∈B(n)
⇒n∈{0;-18}
Đúng 0
Bình luận (0)
Giải:
Ta gọi tích hai số là A
Ta có:
\(A=\dfrac{19}{n-1}.\dfrac{n}{9}=\dfrac{19.n}{\left(n-1\right).9}\) (với n ≠ 1)
Vì \(ƯCLN\left(19;9\right)=1\) \(;ƯCLN\left(n;n-1\right)=1\)
\(\Rightarrow A\in Z\)
\(\Rightarrow n\in B\left(9\right)\) và \(\left(n-1\right)\inƯ\left(19\right)\)
Ta có bảng giá trị:
| n-1 | 1 | -1 | 19 | -19 |
| n | 2 | 0 | 20 | -18 |
\(\Rightarrow n\in\left\{-18;0\right\}\) (t/m)
Vậy \(n\in\left\{-18;0\right\}\)
Đúng 0
Bình luận (0)
Tìm n thuộc Z để hai phân số \(\frac{19}{n-1}\)(với n khác 1) và \(\frac{n}{9}\)có giá trị là số nguyên ?
Tìm n \(\in\) Z để tích hai phân số \(\frac{19}{n-1}\) (với n\(\ne\)1) và\(\frac{n}{9}\) có giá trị là số nguyên?
Ai giải nhanh nhất và dễ hiểu thì mk tích cho!
Để \(\frac{19}{n-1}.\frac{n}{9}\in Z\) thì 19n chia hết cho 9( n - 1 ) ( 1 )
Từ ( 1 ) => 19n chai hết cho 9, mà ƯCLN ( 19,9 ) = 1 => n chia hết cho 9
Từ ( 1 ) => 19n chia hết cho n - 1, mà ƯCLN ( n ; n - 1 ) = 1 => 19 chia hết cho n - 1
\(\Rightarrow n-1\inƯ\left(19\right)=\left\{-9;-1;1;9\right\}\)
\(\Rightarrow n\in\left\{0;2;-18;20\right\}\)
Mà n chia hết cho 9
\(\Rightarrow n\in\left\{0;-18\right\}\)
Đúng 0
Bình luận (0)
Tìm n thuộc z để tích hai phân số 19/n-1 (với n khác 1) và n/9 có giá trị là số nguyên
tìm n thuộc z để tích hai phân số 19 phần n trừ 1 với n khác 1 và N phân 9 có giá trị là số nguyên
Ta có 19 / n - 1 . n / 9 = 19 . n / ( n -1 ) . 9 (với n không bằng 1)
Vì ƯCLN ( 19 , 9 ) = 1 ; ( n ; n - 1 ) = 1 nên muốn cho tích 19 . n / ( n - 1 ) . 9có giá trị số nguyên thì n phải là bội của 9, còn n - 1 phải là ước của 19. Lập bảng số:
n - 1 1 -1 19 -19
n 2 0 20 -18
Chỉ có số n = 0 và n = -18 thỏa mãn là bội của 9. Vậy n thuộc { 0 ; -18 }
Đúng 0
Bình luận (0)
https://cdn2.olm.vn/images/avt/avt0/avt497380_60by60.jpg?v=1
Tìm n thuộc Z để tích hai phân số \(\frac{19}{n-1}\) và \(\frac{n}{9}\) có giá trị là số nguyên. ( n khác 1)
Tìm n thuộc Z để tích hai phân số 19 / n - 1 ( với n không bằng 1 ) và n / 9 có giá trị là số nguyên?
Ta có 19 / n - 1 . n / 9 = 19 . n / ( n -1 ) . 9 (với n không bằng 1)
Vì ƯCLN ( 19 , 9 ) = 1 ; ( n ; n - 1 ) = 1 nên muốn cho tích 19 . n / ( n - 1 ) . 9có giá trị số nguyên thì n phải là bội của 9, còn n - 1 phải là ước của 19. Lập bảng số:
n - 1 | 1 | -1 | 19 | -19 |
| n | 2 | 0 | 20 | -18 |
Chỉ có số n = 0 và n = -18 thỏa mãn là bội của 9. Vậy n thuộc { 0 ; -18 }
Đúng 0
Bình luận (0)
Bạn Nguyễn Phi Hòa làm đúng rồi n thuộc{0;-18}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm n thuộc Z để tích hai phân số 19 / n - 1 ( với n không bằng 1 ) và n / 9 có giá trị là số nguyên?