Cho tam giác ABC có = 1200 cạnh b = 8cm và c = 5cm. Tính cạnh a, và góc
,
của tam giác đó.

Những câu hỏi liên quan
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
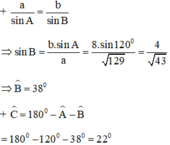
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{A}=120^0\), cạnh b = 8cm và cạnh c = 5cm. Tính cạnh a và các góc \(\widehat{B,}\widehat{C}\) của tam giác đó ?
a2 = 82 + 52 - 2.8.5 cos 1200 = 64 + 25 + 40 = 129
=> a = √129 ≈ 11, 36cm
Ta có thể tính góc B theo định lí cosin
cosB = =
≈ 0,7936 =>
= 37048’
Ta cũng có thể tính góc B theo định lí sin :
cosB = =
=> sinB ≈ 0,6085 =>
= 37048’
Tính C từ = 1800- (
+
) =>
≈ 22012’
Đúng 0
Bình luận (0)
Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.
a) Tam giác đó có góc tù không?
b) Tính độ dài trung tuyến MA của tam giác ABC đó.
a) Ta có:
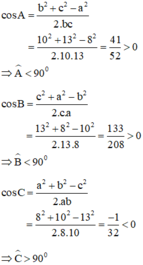
Vậy tam giác ABC có góc C tù.
b) Ta có:
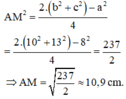
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có cạnh AB = 5cm, cạnh huyền dài hơn AC là 1cm.
a, Tính các tỉ số lượng giác của các góc B và C.
b, Tìm số đo các góc của tam giác ABC.
cho tam giác abc, góc A=90°, góc B =60°, AB=8cm a) tính góc C, cạnh Ac và BC b) tính diện tích tam giác ABC
Ta có \(\widehat{A}=90^0\Rightarrow\Delta ABC\) vuông tại \(A\)
\(a,\widehat{C}=90^0-\widehat{B}=30^0\\ AC=\tan B\cdot AB=\tan60^0\cdot8=8\sqrt{3}\left(cm\right)\\ BC=\dfrac{AB}{\sin C}=\dfrac{8}{\sin30^0}=16\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot8\cdot8\sqrt{3}=32\sqrt{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
cho tam giác abc có a=90 độ cạnh ab=6 ac=8cm a) tính cạnh bc , góc b và góc c .b) vẽ tia phân giác góc a cắt bc tại d tính bd và dc
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
=>\(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq37^0\)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)
=>\(DB=\dfrac{30}{7}\left(cm\right);DC=\dfrac{40}{7}\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có A = 120 độ , B=30 độ , đường cao AH=5cm . Tính các cạnh và các góc của tam giác ABC .
Cho tam giác ABC có AB=5cm,AC=7cm,BC=9cm.Hãy tính độ dài các cạnh của tam giác A'B'C' đồng dạng với tam giác đã cho biết cạnh A'B' tương ứng với cạnh AB và lớn hơn cạnh đó 3cm
Theo giả thiết ta có: \(A'B'=AB+3=5+3=8\left(cm\right)\).
Do \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
\(\Rightarrow\dfrac{7}{A'C'}=\dfrac{9}{B'C'}=\dfrac{5}{8}\Rightarrow\left\{{}\begin{matrix}A'C'=\dfrac{7.8}{5}=\dfrac{56}{5}\left(cm\right)\\B'C'=\dfrac{9.8}{5}=\dfrac{72}{5}\left(cm\right)\end{matrix}\right.\).
Đúng 2
Bình luận (0)
Cho tam giác ABC Có:
A, AB = 5cm , Ac = 7cm ; BC = 8cm Hãy so sánh các góc của tam giác.
B, △Abc có Â = 100độ , B = 300 . Hãy so sánh độ dài 3 cạnh của tam giác đó
a: XétΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< Â\)
b: \(\widehat{C}=180^0-100^0-30^0=50^0\)
Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)
nên AC<AB<BC
Đúng 1
Bình luận (0)
Cho biết tam giác ABC = tam giác HIK, trong đó có AC = 5cm, góc A = 70, góc C = 50. Tính độ dài cạnh HK và số đo góc I của tam giác HIK.
Kiu mina nha!Chúc mina học giỏi!!!!
\(gt\Rightarrow\widehat{B}=\widehat{I}\),\(AC=HK\)mà \(AC=5cm\Rightarrow HK=5cm\)
Trong \(\Delta ABC\)có\(\widehat{A}=70^o,\widehat{C}=50^o\)
Từ đó \(\widehat{B}=60^o\)
Mà \(\widehat{B}=\widehat{I}\Rightarrow\widehat{I}=60^o\)
Vậy \(HK=5cm,\widehat{I}=60^o\)
Đúng 0
Bình luận (0)



















