\(x^2+\left(m-2\right)x-8m\ge0\)

\(\left\{{}\begin{matrix}\Delta\ge0\\x_1+x_2\\x_1x_2\ge0\end{matrix}\right.< 0\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)^2-4\left(-8m\right)\ge0\\-m+2< 0\\-8m\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+4+32m\ge0\\m>2\\m\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(m+14-8\sqrt{3}\right)\left(m+14+8\sqrt{3}\right)\ge0\\m>2\\m\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}\left[{}\begin{matrix}m+14-8\sqrt{3}\ge0\\m+14+8\sqrt{3}\ge0\end{matrix}\right.\\\left[{}\begin{matrix}m+14-8\sqrt{3}\le0\\m+14+8\sqrt{3}\le0\end{matrix}\right.\end{matrix}\right.\\m>2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}\left[{}\begin{matrix}m\ge-14+8\sqrt{3}\\m\ge-14-8\sqrt{3}\end{matrix}\right.\\\left[{}\begin{matrix}m\le-14+8\sqrt{3}\\m\le-14-8\sqrt{3}\end{matrix}\right.\end{matrix}\right.\\m>2\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m\ge-14+8\sqrt{3}\\m\le-14-8\sqrt{3}\end{matrix}\right.\\m>2\end{matrix}\right.\)

\(\Leftrightarrow m>2\)

Vậy ...

Chọn đáp án B

Phương trình đã cho tương đương với:

Xét hàm số f t = t 3 + 3 t trên ℝ

Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên  ℝ

Suy ra

Xét hàm số g x = x + 1 x trên 1 2 ; 2  

Ta có g ' x = 1 - 1 x 2

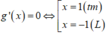
Bảng biến thiên:

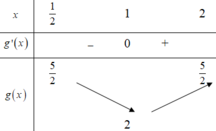
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên  1 2 ; 2

⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x  tại hai điểm phân biệt trên  1 2 ; 2

⇔ 2 < m ≤ 5 2

PT vô nghiệm khi 6mx = 0

<=> m = 0

PT vô nghiệm khi 6m = 0

<=> m = 0

Chọn D

+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x 1 , x 2 , x 3  lập thành một cấp số nhân.

Theo định lý Vi-ét, ta có  x 1 . x 2 . x 3 = 8

Theo tính chất của cấp số nhân, ta có x 1 x 3 = x 2 2 . Suy ra ta có  x 2 3 = 8 ⇔ x 2 = 2.

Với nghiệm x=2, ta có m 2 + 6 m − 7 = 0 ⇔ m = 1 m = − 7  

+ Điều kiện đủ: Với m= 1 hoặc m = -7 thì m 2 + 6 m = 7  nên ta có phương trình:  x 3 − 7 x 2 + 14 x − 8 = 0.

Giải phương trình này, ta được các nghiệm là 1,2,4 Hiển nhiên ba nghiệm này lập thành một cấp số nhân với công bôị q=2

Vậy m= 1 và m=  -7  là các giá trị cần tìm.

Chọn đáp án D.

Bất phương trình tương đương với

trong đó hàm số f t = t 3 + 3 t  đồng biến trên R

Vậy  y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x

Có 5 số nguyên thoả mãn

Bất phương trình tương đương với:

trong đó hàm số f ( t ) = t 3 + 3 t  đồng biến trên R.

Vậy 

Có 5 số nguyên thoả mãn.

Chọn đáp án D.