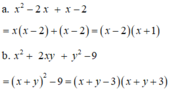chtt

A nhà bn

a: \(-x^2+x+6=-\left(x-3\right)\left(x+2\right)\)

b: Đa thức này ko phân tích được nhé bạn

a: \(-x^2+x+6=-\left(x^2-x-6\right)=-\left(x-3\right)\left(x+2\right)\)

Câu b không phân tích được nhé bạn

Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.

a) x2 – 3x + 2

= x2 – x – 2x + 2 (Tách –3x = – x – 2x)

= (x2 – x) – (2x – 2)

= x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)

= (x – 1)(x – 2)

Hoặc: x2 – 3x + 2

= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)

= x2 – 4 – 3x + 6

= (x2 – 22) – 3(x – 2)

= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)

= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)

b) x2 + x – 6

= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)

= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)

= (x + 3)(x – 2)

c) x2 + 5x + 6 (Tách 5x = 2x + 3x)

= x2 + 2x + 3x + 6

= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung)

= (x + 2)(x + 3)

Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)

a) x2 – 3x + 2

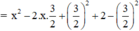
(Vì có x2 và 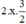 nên ta thêm bớt  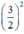để xuất hiện HĐT)

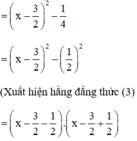
= (x – 2)(x – 1)

b) x2 + x - 6

= (x – 2)(x + 3).

c) x2 + 5x + 6

= (x + 2)(x + 3).

a: \(=-\left(x^2-x-6\right)=-\left(x-3\right)\left(x+2\right)\)

b: Đa thức này không phân tích được nhé bạn

a: \(=-\left(x^2-x-6\right)=-\left(x-3\right)\left(x+2\right)\)

b: Đa thức này không phân tích được nhé bạn

\(M=\frac{2x-1}{x^2-5x+6}=\frac{2x-1}{\left(x-2\right)\left(x-3\right)}=\frac{5\left(x-2\right)-3\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}=\frac{5}{x-3}-\frac{3}{x-2}=\frac{5}{x-3}+\frac{3}{2-x}\)

Bài `1`

\(a,5x^2-10xy=5x\left(x-2y\right)\\ b,3x\left(x-y\right)-6\left(x-y\right)=\left(x-y\right)\left(3x-6\right)\\ =3\left(x-y\right)\left(x-2\right)\\ c,2x\left(x-y\right)-4y\left(y-x\right)=2x\left(x-y\right)+4y\left(x-y\right)\\ =\left(x-y\right)\left(2x+4y\right)=2\left(x-y\right)\left(x+2y\right)\\ d,9x^2-9y^2=\left(3x\right)^2-\left(3y\right)^2=\left(3x-3y\right)\left(3x+3y\right)\\ f,xy-xz-y+z=\left(xy-xz\right)-\left(y-z\right)\\ =x\left(y-z\right)-\left(y-z\right)=\left(y-z\right)\left(x-1\right)\)

Bài `3`

\(a,3x^2+8x=0\\ \Leftrightarrow x\left(3x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x=-8\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{8}{3}\end{matrix}\right.\)

\(b,9x^2-25=0\\ \Leftrightarrow\left(3x\right)^2-5^2=0\\ \Leftrightarrow\left(3x-5\right)\left(3x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-5=0\\3x+5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=5\\3x=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)

\(c,x^3-16x=0\\ \Leftrightarrow x\left(x^2-16\right)=0\\ \Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

\(d,x^3+x=0\\ \Leftrightarrow x\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1\in\varnothing\\x=0\end{matrix}\right.\Rightarrow x=0\)