Bài 21. Một thang máy chuyển động với gia tốc a.một người đứng trong thang máy làm rơi một vật.Tính gia
tốc rơi của vật này trong hai trường hợp.
a) Thang đi lên
b) Thang đi xuống
Help me!!!!
Một người đứng trong một thang máy đang đi xuống nhanh dần đều với gia tốc 11m/s2. Người đó thả rơi một vật ở độ cao 2m so với sàn thang máy. Biết khoảng cách từ trần và san thang máy là 10m, lấy g = 10m/s2. Vật sẽ va vào thang máy sau khi thả rơi vật một khoảng thời gian
A. 4 s
B. 2s
C. 4 21 s
D. 2 11 s
Đáp án A
Chọn hệ quy chiếu gắn với thang máy, chiều dương hướng lên
Gọi sàn thang máy là (1), hòn đá là (2)
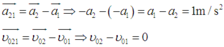
Vậy đối với thang máy vật đi lên nhanh dần đều với gia tốc 1m/s2 , không vận tốc đầu.
Khi vật va vào trần thang máy nó đi được quãng đường
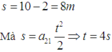
Một thang máy chuyển động lên cao với gia tốc 2 m / s 2 . Lúc thang máy có vận tốc 2,4m/s thì từ trần thang máy có một vật rơi xuống. Trần thang máy cách sàn là h = 2,47m . Hãy tính trong hệ quy chiếu gắn với mặt đất thời gian rơi của vật
A. 0,64s
B. 0,98s
C. 0,21s
D. 1,8s
Chọn A.
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t 2
và của vật là:
y = 2,47 + 2,4t + 0,5g t 2
= 2,47 + 2,4t - 5 t 2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v 0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình :
2,47 + 2,4t - 5 t 2 = 2,4t + t 2
Giải ra và loại nghiệm âm ta được t = 0,64s.
Một thang máy chuyển dộng lên cao vối gia tốc 2 m / s 2 . Lúc thang máy có vận tốc 2,4m/s thì từ trần thang máy có một vật rơi xuống. Trần thang máy cách sàn là h = 2 , 47 m . Hãy tính trong hệ quy chiếu gắn với mặt đất thời gian rơi của vật
A. 0,64s.
B. 0,98s.
C. 0,21s.
D. 1,8s.
Chọn A.
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t2
và của vật là: y = 2,47 + 2,4t + 0,5gt2 = 2,47 + 2,4t - 5t2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình :
2,47 + 2,4t - 5t2 = 2,4t + t2
Giải ra và loại nghiệm âm ta được t = 0,64s.
Một thang máy chuyển dộng lên cao vối gia tốc 2m/s2. Lúc thang máy có vận tốc 2,4m/s thì từ trần thang máy có một vật rơi xuống. Trần thang máy cách sàn là h = 2,47m . Hãy tính trong hệ quy chiếu gắn với mặt đất thời gian rơi của vật
A. 0,64s.
B. 0,98s.
C. 0,21s.
D. 1,8s.
Đáp án A
Chọn hệ quy chiếu gắn với mặt đất, chọn gốc tọa độ là một điểm ngang bằng với sàn A, chọn t = 0 tại thời điểm vật bắt đầu rơi thì phương trình chuyển động của của sàn là:
y = 2,4t + t2
và của vật là: y = 2,47 + 2,4t + 0,5gt2 = 2,47 + 2,4t - 5t2
(Gia tốc có dấu âm vì chuyển động của vật là đi lên chậm dần đều với vận tốc ban đầu là v0 = 2,4m/s)
Vật chạm sàn sau thời gian t là nghiệm của phương trình:
2,47 + 2,4t - 5t2 = 2,4t + t2
Giải ra và loại nghiệm âm ta được t = 0,64s
Một thang máy chuyển dộng lên cao vối gia tốc 2m/s2. Lúc thang máy có vận tốc 2,4m/s thì từ trần thang máy có một vật rơi xuống. Trần thang máy cách sàn là h = 2,47m . Hãy tính trong hệ quy chiếu gắn với mặt đất thời gian rơi của vật
Thang máy có khối lượng 1tấn chuyển động có đồ thị vận tốc như hình vẽ.Tính lực căng của dây cáp treo thang máy trong từng giai đoạn chuyển động.
Xét hai trường hợp:
a. Thang máy đi lên
b. Thang máy đi xuống
c. Biết rằng trong buồng thang máy nêu trên có một người khối lượng 80kg đứng trên sàn. Khi thang máy đi xuống tìm trọng lượng của người trong từng giai đoạn chuyển động của thang máy. Khi nào trọng lượng của ngừơi bằng 0?
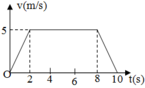
Gia tốc của vật trong từng giai đoạn chuyển động
+ GĐ 1: a 1 = v 2 − v 1 t 1 = 5 − 0 2 = 2 , 5 m / s 2
+ GĐ 2: a 2 = v 3 − v 2 t 2 = 5 − 5 8 = 0 m / s 2
+ GĐ 3: a 3 = v 2 − v 2 t 3 = 0 − 5 2 = − 2 , 5 m / s 2
a. + Giai đoạn 1: Thang máy đi lên nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
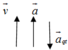
⇒ g / = 10 + 2 , 5 = 12 , 5 m / s 2 ⇒ T = P / = m g / = 1000.12 , 5 = 12500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2
⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi lên chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t

⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
b. Thang máy đi xuống
+ Giai đoạn 1: Đi xuống nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t
⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ T = P / = m g / = 1000.7 , 5 = 7500 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2 ⇒ T = P = m g = 1000.10 = 10000 N
+ Giai đoạn 3: Đi xuống chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
c. Thang máy đi xuống
+ Giai đoạn 1: Đi xuống nhanh dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↑ ↓ g → ⇒ g / = g − a q t
⇒ g / = 10 − 2 , 5 = 7 , 5 m / s 2 ⇒ N = P / = m g / = 80.7 , 5 = 600 N
+ Giai đoạn 2: Vì thang máy chuyển động thẳng đều nên a = 0 m / s 2 ⇒ T = P = m g = 80.10 = 800 N
+ Giai đoạn 3: Đi xuống chậm dần đều với gia tốc 2 , 5 m / s 2 ⇒ a → q t ↓ ↓ g → ⇒ g / = g + a q t
⇒ g / = 10 + 2 , 5 = 12 , 5 m / s 2 ⇒ N = P / = m g / = 80.12 , 5 = 1000 N
Để trọng lượng của ngừơi bằng 0 khi
P / = 0 ⇒ g / = 0 ⇒ a → q t ↑ ↓ g → a q t = g
Tức là lúc này thang máy rơi tự do.
Một thang máy chuyển động với gia tốc a nhỏ hơn gia tốc trọng trường g tại nơi đặt thang máy. Trong thang máy có một con lắc đơn dao động nhỏ. Chu kì dao động nhỏ của con lắc khi thang máy đứng yên bằng 1,1 lần chu kì của con lắc khi thang máy chuyển động. Vecto gia tốc của thang máy là
A. Hướng thẳng đứng lên trên và có độ lớn 0,21 g
B. Hướng thẳng đứng lên trên và có độ lớn 0,17 g
C. Hướng thẳng đứng xuống dưới và có độ lớn 0,21 g
D. Hướng thẳng đứng xuống dưới và có độ lớn 0,17 g
Một thang máy chuyển động với gia tốc nhỏ hơn gia tốc trọng trường g tai nơi đặt thang máy. Trong thang máy có con lắc đơn dao động nhỏ. Chu kì dao động của con lắc khi thang máy đứng yên bằng 1,1 lần khi thang máy chuyển động. Điều đó chứng tỏ vecto gia tốc của thang máy
A. hướng lên trên và độ lớn là 0,11g.
B. hướng lên trên và có độ lớn là 0,21g.
C. hướng xuống dưới và có độ lớn là 0,11g.
D. hướng xuống dưới và có độ lớn là 0,21g.
Một thang máy chuyển động với gia tốc nhỏ hơn gia tốc trọng trường g tai nơi đặt thang máy. Trong thang máy có con lắc đơn dao động nhỏ. Chu kì dao động của con lắc khi thang máy đứng yên bằng 1,1 lần khi thang máy chuyển động. Điều đó chứng tỏ vecto gia tốc của thang máy
A. hướng lên trên và độ lớn là 0,11g
B. hướng lên trên và có độ lớn là 0,21g
C. hướng xuống dưới và có độ lớn là 0,11g
D. hướng xuống dưới và có độ lớn là 0,21g
Đáp án B
Chu kì của con lắc khi thang máy đứng yên lớn hơn chu kì của con lắc khi thang máy chuyển động → F q t cùng chiều với trọng lực → thang máy chuyển động đi lên
Ta có

![]()