Bài 2: 

a: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)

\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{CFE}=60^0\\\widehat{AEB}=\widehat{CEF}=60^0\end{matrix}\right.\)

=>ΔCFE đều

b: Xét tứ giác ABCD có 

\(\widehat{BAC}=\widehat{BDC}=90^0\)

Do đó: ABCD là tứ giác nội tiếp

Bài 1:

a.

AB // CD

=> A + D = 180⁰ (2 góc trong cùng phía)

=> A = 180⁰ - D = 180⁰ - 54⁰ = 126⁰

AB // CD

=> B + C = 180⁰ (2 góc trong cùng phía)

=> B = 180⁰ - C = 180⁰ - 105⁰ = 75⁰

b.

AB // CD 

=> A + D = 180⁰ (2 góc trong cùng phía)

=> A = (180⁰ - 32⁰) : 2 = 74⁰

=> D = 180⁰ - 74⁰ = 106⁰

AB // CD

=> B + C = 180⁰ (2 góc trong cùng phía)

=> B = 180⁰ : (1 + 2) . 2 = 120⁰

=> C = 180⁰ - 120⁰ = 60⁰

Bài 2: 

a: Xét ΔABE và ΔACF có

góc ABE=góc ACF

AB=AC

góc A chung

Do đó: ΔABE=ΔACF

Suy ra: AE=AF

b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC

=>BFEC là hình thang

mà CF=BE

nên BFEC là hình thang cân

c: Xét ΔFEB có góc FEB=góc FBE

nên ΔFEB cân tại F

=>FE=FB=EC

Bài 5

\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)

\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)

\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)

\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)

Xét tg ADE có

\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)

\(\Rightarrow Ax\perp Dy\)

Bài 6:

a/

Ta có

AB//CD => AB//DE

BE//AB (gt)

=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)

b/

CD - DE = CE

Mà AB = DE (cmt)

=> CD - AB = CE

c/

Xét tg BCE có

BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)

Mà CE = CD - DE và DE = AB (cmt) và BE = AD

=> BC+BE = BC + AD>CE = CD - AB

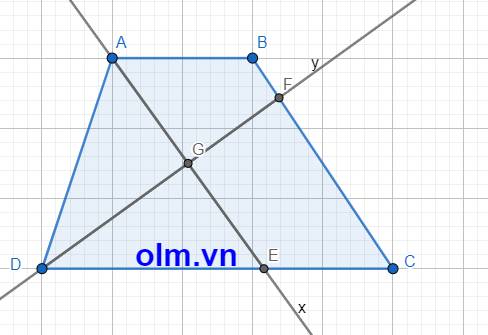
Gọi G là giao điểm của hai đường phân giác Ax và By 

Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)

           \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )

     ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\)) 

           \(\widehat{ADE}\) + \(\widehat{DAB}\) = 180⁰ (vì hai góc là hai góc trong cùng phía)

      ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 180⁰ = 90⁰

          Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 180⁰ (tổng ba góc trong 1 tam giác bằng 180⁰)

               ⇒ \(\widehat{DGA}\)  = 180⁰ - 90⁰ = 90⁰

Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)

                                                           Bài giải

Trong hình thang ABCD có : \(AB\text{ }//\text{ }CD\text{ }\Rightarrow\text{ }\widehat{A}\text{ và }\widehat{D}\text{ là hai góc trong cùng phía }\)

\(\Rightarrow\text{ }\widehat{A}+\widehat{D}=180^o\text{ }\Rightarrow\text{ }\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{D}=\frac{1}{2}\cdot180^o\text{ }\Rightarrow\text{ }\widehat{A_1}+\widehat{D_1}=90^o\)

Trong \(\Delta AOD\) có : \(\widehat{A_1}+\widehat{O}+\widehat{D_1}=180^o\) Mà \(\text{ }\widehat{A_1}+\widehat{D_1}=90^o\text{ }\Rightarrow\text{ }\widehat{O}=90^o\)

\(\Rightarrow\text{ }Ax\text{ }\perp\text{ }Dx\text{ ( }ĐPCM\text{ )}\)

Answer:

A) Ta có: AD // BC

\(\Rightarrow\widehat{ABC}+\widehat{BAD}=180^o\) (Hai góc trong cùng phía bù nhau)

\(\Rightarrow60^o+\widehat{BAD}=180^o\)

\(\Rightarrow\widehat{BAD}=120^o\)

\(\Rightarrow\widehat{BAC}+\widehat{DAC}=120^o\)

\(\Rightarrow\widehat{DAC}=30^o\)

B) Xét tam giác DAC có: DA = DC => Tam giác DAC cân tại D

\(\Rightarrow\widehat{DCA}=\widehat{DAC}=30^o\)

\(\Rightarrow\widehat{DCB}=\widehat{DCA}+\widehat{ACB}=60^o=\widehat{ABC}\)

Tứ giác ABCD có:

AD // BC (giả thiết)

Hai góc kề đáy CD bằng nhau

=> ABCD là hình thang cân

C) Theo phần b): ABCD là hình thang cân

=> AB = CD mà AD = CD (giả thiết)

=> AB = AD

Tam giác ABC vuông tại A có AB là cạnh đối diện \(\widehat{BCA}=30^o\)

=> AB = BC : 2 = BE = EC

Mà ta có: AB = AD => AD = BE

Tứ giác ADEB có:

AD // BE

AD = BE

=> Nên là hình bình hành

Ta có: AD = AB => ADEB là hình thoi