cho tam giác ABC vuông cân tại A đường cao AH trên tia AH lấy M sao cho MH=AH =1/2 AM chứng minh BM vuông góc

Những câu hỏi liên quan
CHO TAM GIÁC ABC VUÔNG TẠI A( AB< AC ) . VẼ ĐƯỜNG CAO AH CỦA TAM GIÁC ABC. TRÊN ĐOẠN AH LẤY ĐIỂM M SAO CHO BM=AB. TIA PHÂN GIÁC CỦA GÓC ABC CẮT AH TẠI N , CẤT AM TẠI E . CHỨNG MINH RẰNG :
A) AM LAFTIA HÂN IACS CỦA GÓC HAC
B) MH VUÔNG GÓC AB
GIÚP MIK VỚI Ạ , MIK SẼ TICK 20 TICK CHO Ạ
Cho tam giác ABC vuông tại A (AB AC), đường cao AH. Trên cạnh BC lấy điểm M sao cho BA BM. .a) Chứng minh AM là tia phân giác của
H
A
C
^
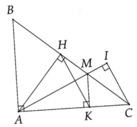
.b) Gọi K là hình chiếu vuông góc của M trên AC. Chứng minh AM là trung trực của HK.c) Gọi I là hình chiếu vuông góc của C trên tia AM. Chứng minh AH, KM, CI đồng quy.d) Chứng minh AB + AC AH + B
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh BC lấy điểm M sao cho BA = BM. .
a) Chứng minh AM là tia phân giác của H A C ^ .
b) Gọi K là hình chiếu vuông góc của M trên AC. Chứng minh AM là trung trực của HK.
c) Gọi I là hình chiếu vuông góc của C trên tia AM. Chứng minh AH, KM, CI đồng quy.
d) Chứng minh AB + AC < AH + B
Cho tam giác ABC cân tại A.Kẻ AH vuông góc BC tại H .Trên tia đối của HA lấy điểm M sao cho AH=HM. a) Chứng minh tam giác ABH=tam giác MBH. b) Trên tia đối của tia CA lấy điểm N sao cho CA=CN.Chứng minh tam giác CMN cân. c) Chứng minh AM vuông góc với MN.
a,Ta có:
\(AH\perp BC\) nên \(\widehat{AHB}\) +90 độ.
Vì M là tia đối của HA nên \(\widehat{MHB}\)= 90 độ.
Xét \(\Delta ABH\) và \(\Delta MBH\)có
AH = MH (gt)
\(\widehat{AHB}\) = \(\widehat{MHB}\) (= 90 độ )
BH : cạnh chung
\(\Rightarrow\Delta ABH=\Delta MBH\)( c.g.c )
b,Xét \(\Delta AHCv\text{à}\Delta MHC\)Ta có:
AH = HM (gt)
\(\widehat{AHC}\)= \(\widehat{MHC}\)(= 90 độ)
HC : cạnh chung
\(\Rightarrow\Delta AHC=\Delta MHC\)( c.g.c)
\(\Rightarrow\)AC=CM ( t/ứ)
Mà AC = CN (gt) và CM = AC (cmt)
nên CM = CN
\(\Rightarrow\Delta CMN\)cân
Cho tam giác ABC vuông tại A có đường cao AH. Trên cạnh BC lấy điểm M sao cho CM = CA. Trên cạnh AB lấy điểm N sao cho AN = AH. Chứng minh
a, Góc CAM = góc CMA
b, AM là tia phân giác của góc BAH
c, Chứng minh MN vuông góc với AB và MH < MB
Hình thì bạn tự vẽ nha
a . Do CM = CA
=> tam giác MCA cân tại C
=> góc CAM = góc CMA ( 2 góc ở đáy )
b .
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC, vuông tại A (ABAC). Trên tia đối của tia AC lấy ddiemr D sao cho AD AB. Trên tia đối của tia AB lấy điểm E sao cho AE AC.a) Chứng minh: BC DEb) Chứng minh: tam giác ABD vuông cân và BD//CE.c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M, từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N. Chứng minh: NM // AB.d) Chứng minh: AM DE/2.
Đọc tiếp
Cho tam giác vuông ABC, vuông tại A (AB<AC). Trên tia đối của tia AC lấy ddiemr D sao cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC.
a) Chứng minh: BC = DE
b) Chứng minh: tam giác ABD vuông cân và BD//CE.
c) Kẻ đường cao AH của tam giác ABC tia AH cắt cạnh DE tại M, từ A kẻ đường vuông góc CM tại K, đường thẳng này cắt BC tại N. Chứng minh: NM // AB.
d) Chứng minh: AM = DE/2.
giúp mk câu c vớiiiiiiiiii
cho tam giác ABC cân ( góc A < 90 độ) đường cao AH. Trên tia đối của tia BC lấy điểm D sao cho BD = BA. Kẻ BM vuông góc AD ( M thuộc AD)
tam giác AHD đồng dạng với tam giác BMD
DB. DH = DA ^2/2
c, Tia MH cắt tia AC tại N. Chứng minh : tam giác ADB đồng dạng với tam giác NCH và CH = CN
c:Xét ΔABD và ΔNCH có
góc ABD=góc NCH
góc D=góc NHC
=>ΔABD đồng dạng với ΔNCH
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A. Gọi BM là tia phân giác của góc ABC (M thuộc AC). Trên tia BC lấy điểm H sao cho BA = BH.
a) Chứng minh: tam giác ABM = tam giác HBM
b) Chứng minh: MH vuông góc với BC
c) Tia BK cắt tia HM tại K. Chứng minh tam giác KMC cân tại M
d) Chứng minh: AH vuông góc với KC
4)cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy điểm N sao cho BMCN a) chứng minh: tam giác ABM tam giác ACN b) kẻ BH vuông góc AM; CK vuông góc AN(H thuộc AM;K thuộc AN). chứng minh: AHAK c) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? vì sao ?5)tìm các số x,y,z biết: dfrac{3x-2y}{4}dfrac{2z-4x}{3}dfrac{4y-3z}{2}và x+y+z-20
Đọc tiếp
4)cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy điểm N sao cho BM=CN
a) chứng minh: tam giác ABM = tam giác ACN
b) kẻ BH vuông góc AM; CK vuông góc AN(H thuộc AM;K thuộc AN). chứng minh: AH=AK
c) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì ? vì sao ?
5)tìm các số x,y,z biết: \(\dfrac{3x-2y}{4}\)=\(\dfrac{2z-4x}{3}\)=\(\dfrac{4y-3z}{2}\)và x+y+z=-20
a) \(\Delta ABC\) cân tại A (gt).
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\widehat{ABC}=\widehat{ACB}\end{matrix}\right.\) (Tính chất tam giác cân).
Mà \(\widehat{ABC}+\widehat{ABM}=180^o;\widehat{ACB}+\widehat{ACN}=180^o.\)
\(\Rightarrow\widehat{ABM}=\widehat{ACN}.\)
Xét \(\Delta ABM\) và \(\Delta ACN:\)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right).\\ MB=CN\left(gt\right).\\ AB=AC\left(cmt\right).\)
\(\Rightarrow\) \(\Delta ABM\) \(=\) \(\Delta ACN\left(c-g-c\right).\)
b) Xét \(\Delta ABH\) và \(\Delta ACK:\)
\(AB=AC\left(cmt\right).\\ \widehat{AHB}=\widehat{AKC}\left(=90^o\right).\\ \widehat{HAB}=\widehat{KAC}\left(\Delta ABM=\Delta ACN\right).\)
\(\Rightarrow\Delta ABH=\Delta ACK\) (cạnh huyền - góc nhọn).
\(\Rightarrow\) AH = AK (2 cạnh tương ứng).
c) Xét \(\Delta AOH\) và \(\Delta AOK:\)
\(AH=AK\left(cmt\right).\\ AOchung.\\ \widehat{AHO}=\widehat{AKO}\left(=90^o\right).\)
\(\Rightarrow\) \(\Delta AOH\) \(=\) \(\Delta AOK\) (cạnh huyền - cạnh góc vuông).
\(\Rightarrow\) OH = OK (2 cạnh tương ứng).
Mà \(\left\{{}\begin{matrix}OB=OH-HB;OC=OK-KC.\\HB=KC\left(\Delta ABH=\Delta ACK\right).\end{matrix}\right.\)
\(\Rightarrow\) OB = OC.
\(\Rightarrow\Delta OBC\) cân tại O.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Vẽ AH là đường cao của tam giác ABC. a. Chứng minh ∆AHB= ∆AHC. b. Từ H vẽ HD vuông góc AB (D thuộc AB). Trên tia đối tia DH lấy điểm M sao cho DH = DM. Chứng minh AM=AH c. Gọi K là trung điểm của AM. Gọi I là giao điểm của AD và HK. Tia MI cắt AH tại N. Chứng minh: AM AN 2
a) Vì ∆ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến
Suy ra BH=CH
Xét ∆AHB và ∆AHC có
AH là cạnh chung
BH=CH (cmt)
AB=AC (∆ABC cân tại A)
Do đó ∆AHB=∆AHC
Xét ∆AMH ta có
AD vuông góc với MH (HD vuông góc AB)
Suy ra AD là đường cao của ∆AMH (1)
DH=DM (gt)
Nên AD là đường trung bình của ∆AMH (2)
Từ (1) và (2) suy ra ∆AMH cân tại A
Suy ra AM=AH