Tìm gt lớn nhất của bt : -x2 + 2x - 3

Những câu hỏi liên quan
1). Tìm số nguyên n sao cho 2n^2 +n - 7 chia hết cho n-2
2). Tìm gt lớn nhất của bt : -x^2 + 2x - 3
1) \(2n^2+n-7=2n^2-4n+5n-10+3=2n\left(n-2\right)+5\left(n-2\right)+3=\left(n-2\right)\left(2n+5\right)+3\)ta có: (n-2)(2n+5) đã chia hết cho n-2 => để biểu thức chia hết cho n-2 <=> 3 chia hết cho n-2 <=> n-2 thuộc Ư(3) <=> n-2 thuộc (+-1;+-3) <=> n thuộc(3;1;5;-1)
2) \(=-\left(x^2-2x+1+2\right)=-2-\left(x-1\right)^2\le-2\Rightarrow Max=-2\Leftrightarrow x=1\)
Đúng 0
Bình luận (0)
A=\(\frac{2\left(n+1\right)+5}{n+1}\)\(2+\frac{5}{n+1}\)
A là số nguyên nếu \(\frac{5}{n+1}\)là số nguyên. Do n thuộc Z nên n+1 Là ước của 5
Ta có bảng sau
| n+1 | 1 | -1 | 5 | -5 |
| n | 0 | -2 | 4 | -6 |
| A | 7 | -3 | 3 | 1 |
Đúng 0
Bình luận (0)
Cho bt A= ( 1/x-2 - 2x/4-x2 + 1/2=x ) * (2/x-1) a, Rút gọn A b, Tính gt của bt a tại x=4 và x=2 C, Tìm x nguyên để A= 1/3
Tìm giá trị nguyên lớn nhất của m để:
x
2
-
2
x
-
3
+
8
+
2
x
-
x
2
m
,
(
*
)
có nghiệm A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Tìm giá trị nguyên lớn nhất của m để: x 2 - 2 x - 3 + 8 + 2 x - x 2 > m , ( * ) có nghiệm
A. 1
B. 2
C. 3
D. 4
Điều kiện: 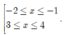
Đặt t= x2- 2x; t’ = 2x- 2 và t’ =0 khi x= 1.
Bảng biến thiên
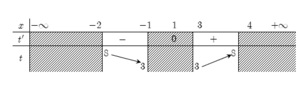
Dựa vào bảng biến thiên suy ra tập giá trị của t là [ 3; 8].
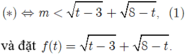
Để (* ) có nghiệm khi và chỉ khi ( 1) có nghiệm
![]()
Xét hàm số
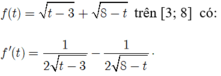
Cho f’ (t) =0 khi nên
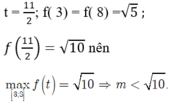
Vậy m ∈ (-∞; √10) sẽ thỏa mãn yêu cầu bài toán.
Chọn D.
Đúng 0
Bình luận (0)
cho X, y>=0 sao cho X2+ Y2=1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của A= √2X+1+√2Y+1
với x;y>=0 ta có:
\(A^2=\left(\sqrt{2x+1}+\sqrt{2y+1}\right)^2=2x+1+2y+1+2\sqrt{\left(2x+1\right)\left(2y+1\right)}\)
\(=2\left(x+y\right)+2+\sqrt{4xy+2x+2y+1}=2\left(x+y\right)+2+\sqrt{4xy+2\left(x+y\right)+1}\)
\(2=2\left(x^2+y^2\right)=\left(1+1\right)\left(x^2+y^2\right)>=\left(x+y\right)^2\Rightarrow x+y< =\sqrt{2}\)(bđt bunhiacopxki)
\(2xy< =x^2+y^2=1\Rightarrow2\cdot2xy=4xy< =2\cdot1=2\)
\(\Rightarrow A^2=2\left(x+y\right)+2+2\sqrt{4xy+2\left(x+y\right)+1}< =2\sqrt{2}+2+2\sqrt{2+2\sqrt{2}+1}\)
\(=2\sqrt{2}+2+2\sqrt{\left(\sqrt{2}+1\right)^2}=2\sqrt{2}+2+2\left(\sqrt{2}+1\right)4\sqrt{2}+4\)
\(\Rightarrow A< =\sqrt{4\sqrt{2}+4}\)
dấu = xảy ra khi x=y=\(\sqrt{\frac{1}{2}}\)
vậy max A là \(\sqrt{4\sqrt{2}+4}\)khi \(x=y=\sqrt{\frac{1}{2}}\)
Đúng 0
Bình luận (0)
a) tìm gt lớn nhất của bt: 2 + x - x^2.
b) tìm gt nhỏ nhất của bt : 4x^2 - 20x +26
giải hộ vs ạ > cảm ơn nhìu
a, Đặt \(A=2+x-x^2=-\left(x^2-x-2\right)=-\left(x^2-x+\frac{1}{4}-\frac{9}{4}\right)=-\left(x-\frac{1}{2}\right)^2+\frac{9}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow-\left(x-\frac{1}{2}\right)^2\le0\Rightarrow A=-\left(x-\frac{1}{2}\right)^2+\frac{9}{4}\le\frac{9}{4}\)
Dấu "=" xảy ra khi x = 1/2
Vậy Amax=9/4 khi x=1/2
b, Đặt \(B=4x^2-20x+26=\left(2x\right)^2-2.2x.5+25+1=\left(2x-5\right)^2+1\)
Vì \(\left(2x-5\right)^2\ge0\Rightarrow B=\left(2x-5\right)^2+1\ge1\)
Dấu "=" xảy ra khi x = 5/2
Vậy Bmin=1 khi x=5/2
Đúng 0
Bình luận (0)
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của bt
\(y=\frac{x^2+2x+3}{2x^2-x+4}\)
Nhân chéo y lên trừ đi rồi dùng denta là xong,dễ lắm
Đúng 0
Bình luận (0)
y>0 với mọi x suy ra 2x^2y-xy+4y=x^2+2x+3>>>(2y-1)x^2-(y-2)x+(4y-3)=0(1)
Xét 2y-1=0 suy ra y=1/2 suy ra x=2/3(1)
Xét 2y-1 khác 0 pt trơ thành pt bậc 2 ẩn x suy ra delta=(y-2)^2-4(4y-3)(2y-1)>=0
suy ra 31y^2-36y+8<=0 rồi tìm được khoảng của y rồi so sánh với (1) là y=1/2 ta sẽ có GTLN và GTNN của y
Đúng 0
Bình luận (0)
15,tìm các gt nhỏ haowjc lớn nhất của bt sau
d = 2 trên -x2-7
e = 7 trên -x2 - 2x - 15
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.



















