Giải hộ mình bài này với mình đang cần gấp

Những câu hỏi liên quan
Giải hộ mình bài này với mình đang cần gấp 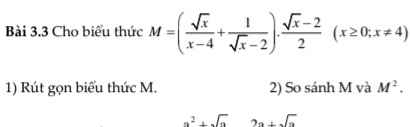
\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
Đúng 1
Bình luận (0)
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
Đúng 0
Bình luận (0)
Bạn nào giải hộ mình 4 bài này với mình đang cần gấp cảm ơn nhiều ạ
Câu 1: Vì (d') vuông góc với (d) nên \(a\cdot\dfrac{-1}{3}=-1\)
hay a=3
Vậy: (d'): y=3x+b
Thay x=4 và y=-5 vào (d'), ta được:
b+12=-5
hay b=-17
Đúng 1
Bình luận (0)
Giải hộ mình con này với,mình đang cần gấp.
Mọi người ơi,có thể giải bài này hộ mình được không mình đang cần gấp mà hơi khó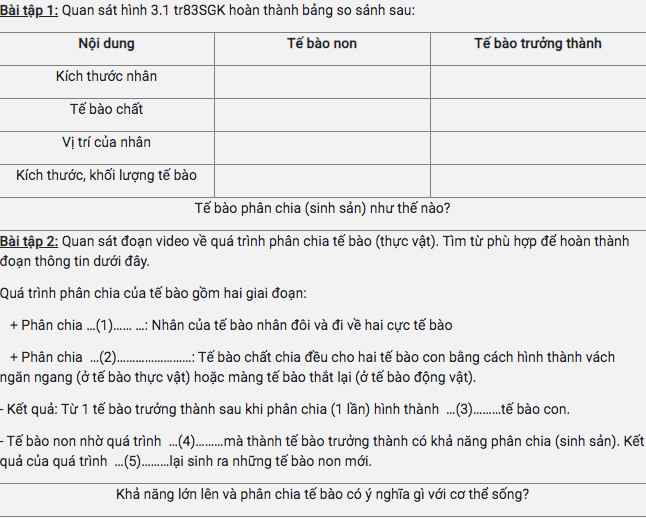
Giải hộ mình bài này với ạ mình cần gấp 
Sửa đề là : 4.6 (g)
\(n_{H_2}=\dfrac{2.24}{22.4}=0.1\left(mol\right)\)
\(A+H_2O\rightarrow AOH+\dfrac{1}{2}H_2\)
\(0.2...............................0.1\)
\(M_A=\dfrac{4.6}{0.2}=23\left(\dfrac{g}{mol}\right)\)
\(A:Na\)
Đúng 2
Bình luận (0)
Đề này C1 em sửa thành 4,6 gam kim loại như bạn dưới, C2 em sửa thành 22,4 lít H2
Đúng 0
Bình luận (0)
Giải hộ mình bài 1.2 với ạ mình đang cần gấp:((
Bài 1.2
1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
2) Ta có: \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}+1}{3-\sqrt{x}}-\dfrac{3-11\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3-11\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3-3+11\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)
Đúng 2
Bình luận (0)
Trong bài thơ BẠN ĐẾN CHƠI NHÀ tác giả gọi bạn là bác, cách xưng hô này có ý nghĩa gì ?
( giải hộ mình với mình đang cần gấp ạ)
cách sưng hô bác-tôi của tác giả thể hiện sự thân thiết đồng thời thể hiện sự kính trọng của tác giả đối với người bạn thân của mình
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
Cách sưng hô bác-tôi có ý nghĩa là : tình bạn thân thiết của tác giả đối với người bạn lâu gặp
Đúng 0
Bình luận (0)
giải chi tiết hộ mình bài này:
1.2.3 + 2.3.4 + 3.4.5 + ... + 99.100.101
mình đang cần gấp
Đặt \(C=1.2.3+2.3.4+3.4.5+...+99.100.101\)
\(4C=1.2.3.4+2.3.4.4+3.4.5.4+...+99.100.101.4\)
\(4C=1.2.3.\left(4-0\right)+2.3.4.\left(5-1\right)+3.4.5.\left(6-2\right)+....+99.100.101.\left(102-98\right)\)
\(4C=1.2.3.4+2.3.4.5+3.4.5.6+...+99.100.101.102\)
\(4C=99.100.101.102=101989800\)
\(\Rightarrow C=\frac{101989800}{4}=25497450\)
Đúng 0
Bình luận (0)
A=1.2.3+2.3.4+3.4.5+4.5.6+...+98.99.100
4A=(1.2.3+2.3.4+3.4.5+4.5.6+...+98.99.100).4
4A=1.2.3(4-0)+2.3.4(5-1)+3.4.5(6-2)+4.5.6(7-3)+...+98.99.100(101-97)
4A=1.2.3.4+2.3.4.5-1.2.3.4+3.4.5.6-2.3.4.5+4.5.6.7-3.4.5.6+...+98.99.100.101-97.98.99.100
4A=1.2.3.4-1.2.3.4+2.3.4.5-2.3.4.5+3.4.5.6-3.4.5.6+...+97.98.99.100-97.98.99.100+98.99.100.101
4A=98.99.100.101
A=98.99.100.101/4
Đúng 0
Bình luận (0)
Giải hộ mình con này với minh đang cần gấp.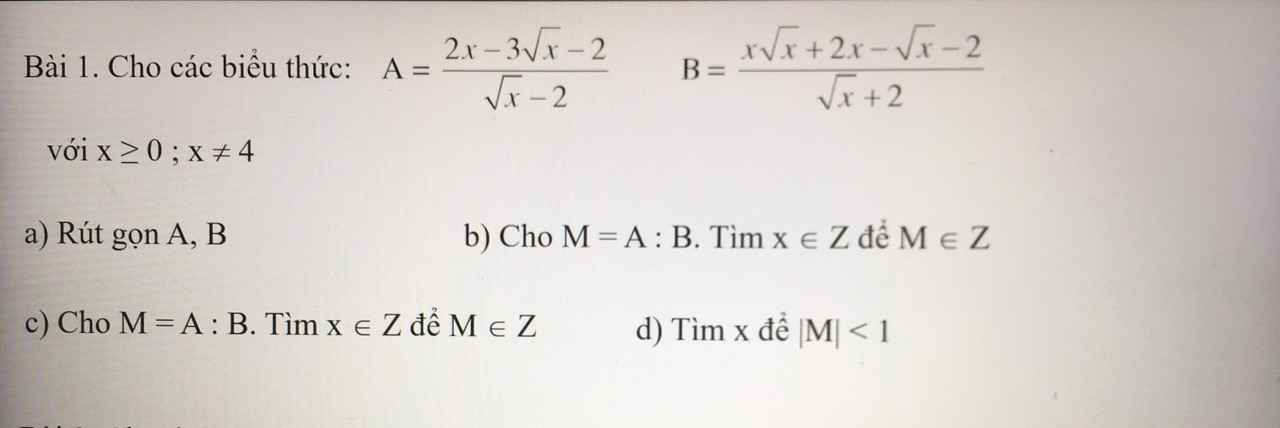
\(a,ĐK:x\ge0;x\ne4\\ A=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}+1\\ B=\dfrac{\left(x-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}+2}=x-1\\ b,M=A:B=\dfrac{2\sqrt{x}+1}{x-1}=\dfrac{2\left(\sqrt{x}+1\right)-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{2}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\\sqrt{x}+1\inƯ\left(1\right)=\left\{-1;1\right\}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\in\left\{0;2;3\right\}\left(\sqrt{x}\ge0\right)\\\sqrt{x}=0\left(\sqrt{x}\ge0\right)\end{matrix}\right.\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)





















