Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với
H qua M. Tính số đo các góc ABK, ACK

Những câu hỏi liên quan
Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo các góc ABK, ACK
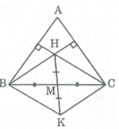
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK, ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
Ta có: CH ⊥ AB (gt)
Suy ra: KB ⊥ AB nên ∠ (KBA) = 90 0
Ta có: BH ⊥ AC (gt)
Suy ra: CK ⊥ AC nên ∠ (KCA) = 90 0
Đúng 0
Bình luận (0)
Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo các góc ABK, ACK ?
Cho tam giác ABC có trực tâm H . Gọi M là trung điểm của BC,K là điểm đối xứng với H qua M.Tính số đo các góc ABK,ACK
2/ Cho tam giác ABC có trực tâm H . Gọi M là trung điểm BC.Tia Bx vuông góc AB và tia Cy vuông góc AC cắt nhau tại D . Chứng minh H và D đối xứng với nhau qua M
Cho tam giác ABC có trực tâm H.Gọi M là trung điểm của BC,K là điểm đối xứng với H qua M.Tính số đo các góc ABK,ACK?
Tam giác ABC có H là trực tâm, M là trung điểm BC. Gọi K là điểm đối xứng với H qua M. Tính các góc ABK và ACK.
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
CH ⊥ AB (gt)
\(\Rightarrow KB\perp AB\Rightarrow\widehat{KBA}=90^0\)
BH ⊥ AC (gt)
\(\Rightarrow CK\perp AC\Rightarrow\widehat{KCA}=90^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A=60°(tam giác ABC không cân).Cạnh BC cố định; trên BC lấy M là trung điểm.H là trực tâm của tam giác ABC .Lấy K đối xứng với H qua M .
Hỏi : 1) góc ABK =? góc ACK=?
2)Chứng minh góc BKC không đổi
Tam giác ABC có O là giao điểm các đường trung trực. H là trực tâm của tam giác ABC. M là trung điểm BC. Gọi K là điểm đối xứng của H qua M. Chứng minh rằng A và K đối xứng nhau qua O
help me please!
Cho tam giác nhọn ABC. Đường cao BE và CF cắt nhau tại H. Gọi M là trung điểm của BC, K là điểm đối ứng với H qua M.
a, Chứng Minh rằng tứ giác BHCK là Hình Bình Hành
b, Tính số đo các góc của ABK và ACK
c, Tam giác ABC cần điều kiện gì để BHCK là hình thoi
a) Có M là td BC
MH = MK ( K đối xứng H qua M)
Suy ra M là td mỗi đg
suy ra BHCK là hbh
Vậy...
b) có ch là đường cao tam giác ABC ( H là trực tâm)
suy ra CH vuông góc AB
có bhck là hình bình hành
=> DK song song với CH
Suy ra DK vuông góc AB
Vậy góc ABK bằng 90 độ
C) BHCK là hình thoi
Khi và chỉ khi BH = CH
Khi và chỉ khi H là trọng tâm của tam giác ABC
Khi và chỉ khi tam giác ABC đều
Vận tam giác ABC đều thì tứ giác BHCK là hình thoi
Biết bạn đề bài này lâu rồi nhưng mà mình cứ giải Xem cách của mình với các của bạn cách nào tiện hơn hihi
Đúng 0
Bình luận (0)
cho tam giác abc. i là giao điểm các đường trung trực, h l à trực tâm, m là trung điểm của bc. gọi k là điểm ddooois xứng với h qua m. cmr k đối xứng vs a qua i
















