giúp mk bài này vs (áp dụng bđt AM-GM)
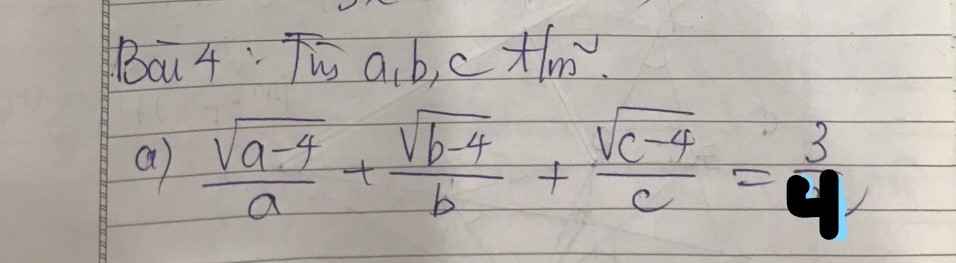
Công thức và cách áp dụng với BĐT AM-GM , bunhiacopxki
Em tham khảo nhé, công thức AM-GM thì điều kiện là các số không âm, còn công thức Bunhiacopxki thì các số thuộc tập hợp số thực là được.


Sử dụng bđt am - gm ạ!

Sử dụng bđt am - gm ạ!
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(< =>\left(\dfrac{1}{a}+\dfrac{1}{b}\right).\left(a+b\right)\ge4\)
\(< =>1+\dfrac{b}{a}+\dfrac{a}{b}+1\ge4\)
\(< =>2+\dfrac{a}{b}+\dfrac{b}{a}\ge4\)(luôn đúng với mọi a,b là số thực dương)
Thật vậy có \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}.\dfrac{b}{a}}=2\)(BĐT Cosi)
\(=>2+\dfrac{a}{b}+\dfrac{b}{a}\ge2+2=4\left(đpcm\right)\)
dấu"=" xảy ra<=>a=b
Ta có $P=\dfrac{x^2}{y-1}+ \frac{y^2}{x-1}$.
Áp dụng BĐT AM-GM ta có $1 \cdot (y-1) \le \frac{y^2}{4} \Rightarrow \frac{x^2}{y-1} \ge \frac{4x^2}{y^2}$.
Tương tự thì $\frac{y^2}{x-1} \ge \frac{4y^2}{x^2}$. Vậy $P \ge \dfrac{4x^2}{y^2}+ \frac{4y^2}{x^2} \ge 8$ theo BĐT AM-GM.
Dấu đẳng thức xảy ra khi và chỉ khi $x=y=2$. $\blacksquare$
Cho mình hỏi lúc làm bài liên quan đến BĐT Cô si dạng Engel ấy ạ, lúc áp dụng BĐT này thì ở trên có cần phải chứng minh không ạ?
xài bđt phụ mới cần phải chứng minh nhé
mà tau nhớ làm gì có Cô si dạng Engel ??? ._.
Ý mày là không tồn tại cái BĐT tên Cosi dạng engel á:")?
Cauchy-Schwarz dạng Engel thì có :)) còn Cauchy dạng Engel chưa nghe bao giờ ???
cho mình hỏi có bđt nào có dạng: abc\(\le\left(\frac{a+b+c}{3}\right)^3\)không ạ?. mình từng thấy có bài áp dụng bđt này nma vẫn không biết nó là bđt phụ hay tên là gì. mình cảm ơn
\(abc\le\left(\frac{a+b+c}{3}\right)^3\Leftrightarrow\sqrt[3]{abc}\le\frac{a+b+c}{3}\)
BĐT Cô- si
đánh giá từ tbn sang tbc đấy bạn
áp dụng xây dựng cơ sở dữ liệu quản lí học sinh?
mn giúp mk giải câu này vs ạ:))
Tham khảo!
Bước 1: Khảo sát
- Tìm hiểu các yêu cầu của công tác quản lí.
- Xác định và phân tích mối liên hệ các dữ liệu cần lưu trữ.
- Phân tích các chức năng cần có của hệ thống khai thác thông tin, đáp ứng các yêu cầu đặt ra.
- Xác định khả năng phần cứng, phần mềm có thể khai thác, sử dụng.
Bước 2: Thiết kế
- Thiết kế CSDL.
- Lựa chọn hệ quản trị để triển khai.
- Xây dựng hệ thống chương trình ứng dụng.
Bước 3: Kiểm thử
- Nhập dữ liệu cho CSDL.
- Tiến hành chạy thử các chương trình ứng dụng.
giúp mình bài này với ( gợi ý : dùng bất đẳng thức AM GM)
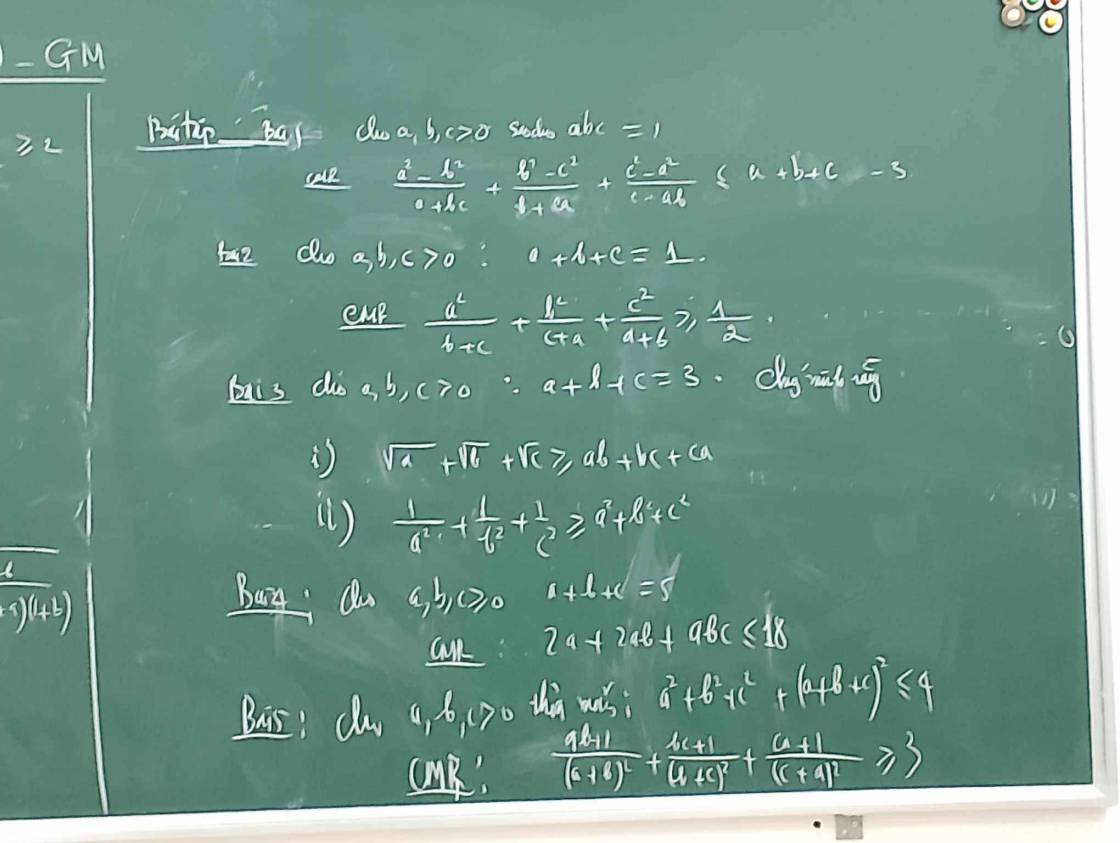
Sử dụng BĐT AM-GM giải bài toán sau:
Cho các số dương a,b,c. CMR: \(3\left(a+b+c\right)^2\le\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)\)
Bài này giải bằng Bunhiacopxki (kết hợp nguyên lý Dirichlet) chứ AM-GM thì e là không ổn:
Theo nguyên lý Dirichlet, trong 3 số \(a^2;b^2;c^2\) luôn có 2 số cùng phía so với 1, không mất tính tổng quát, giả sử đó là \(b^2\) và \(c^2\)
\(\Rightarrow\left(b^2-1\right)\left(c^2-1\right)\ge0\)
\(\Rightarrow b^2c^2+1\ge b^2+c^2\)
\(\Rightarrow b^2c^2+2b^2+2c^2+4\ge3b^2+3c^2+3\)
\(\Rightarrow\left(b^2+2\right)\left(c^2+2\right)\ge3\left(b^2+c^2+1\right)\)
\(\Rightarrow\left(a^2+2\right)\left(b^2+2\right)\left(c^2+2\right)\ge3\left(a^2+1+1\right)\left(1+b^2+c^2\right)\ge3\left(a+b+c\right)^2\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)