Cho tam giác ABC. Ở phía ngoài A vẽ hình vuông ABDE tâm I và ACFH tâm K. Gọi M là trung điểm của BC.
a) tam giác MIK là hình gì?
b) Gọi M là trung điểm của EH tứ giác MNIK là hình gì?
cho tam giác nhọn ABC , vẽ ra phía ngoài cuat tam giác 2 hình vuông ABDE và ACFH , gọi I và K lần lượt là tâm của 2 hình vuông nói trên , M là trung điểm của cạnh BC
a, C/m: EC=BH và EC vuông góc với BH
b, Gọi N là trung điểm của EH. Tứ giác MINK là hình gì? Vì sao?
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH. Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì? Vì sao?
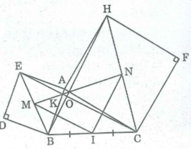
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.
Cho tam giác ABC. Ở phía ngoài tam giác đó vẽ các hình vuông ABDE ,ACFH .gọi M,N,I,K theo thứ tự là trung điểm của EB,BC,CH,HE.C/m: tứ giác MNIK là hình vuông
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.
a) CMR: EC = BH
b) Gọi M, N thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MNI là tamgiacs gì? Vì sao?
( Vẽ hình luôn hộ mk nha )
Cho tam giác ABC. Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH
a) Chứng minh rằng \(EC=BH,EC\perp BH\)
b) Gọi M, N theo thứ tự là tâm của các hình vuông ABDE, ACFH. Gọi I là trung điểm của BC. Tam giác MIN là tam giác gì ? Vì sao ?
Cho tam giác ABC là tam giác nhọn. vẽ ra ngoài 2 hình vuông ABDE và ACFH. Gọi I , K lần lượt là tâm của 2 hình vuông
a) CM EC=BH, EC vuông góc với BH
b) Vẽ N và M lần lượt là trung điểm của EH và BC. Tứ giác MINK là hình gì ? Vì sao?
Giúp mình làm bài này
Mình Like cho
Cho Tam giác ABC, ở ngoài tam giác vẽ hình vuông ABDE,ACFH
a) CMR: EC=BH, EC vuông góc với BH
b) Gọi M,N theo thứ thự là tâm các hình vuông ABDE,ACFH. Gọi I là trung điiểm BC. Tam giác MIN là hình gì? Vì sao?
Cho tam giác nhọn ABCD. Vẽ ra phía ngoài của tam giác 2 hình vuông ABDE và ACFH.Gọi I và K lần lượt là tâm của 2 hình vuông nói trên.
a) Chứng minh EC=BH và EC vuông góc với BH
b) Gọi N là trung điểm của EH, M là trung điểm của BC.Tứ giác MINK là hình gì? Vì sao?
Đề bị sai từ câu đầu tiên. Tam giác chỉ có thể kí hiệu bằng 3 chữ cái in hoa.
Cho tam giác ABC vẽ ở phía ngoài của tam giác dựng các hình vuông ABDE và ACDF .
a ) CMR : EC = BH và EC vuông góc với BH .
b ) Gọi O1 và O2 theo thự tự lần lượt là giao điểm của các đường chéo của các hình vuông ACFH và ABDE . Gọi I là trung điểm của BC . Tam giác O1IO2 là tam giác gì ?
a. Ta thấy \(\widehat{EAC}=\widehat{BAH}\left(=\widehat{BAC}+90^o\right)\)
Vậy nên \(\Delta EAC=\Delta BAH\left(c-g-c\right)\)
Từ đó suy ra \(\widehat{ACE}=\widehat{AHB}\)
Vì \(\widehat{AHB}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{ACE}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{HJC}=90^o\)
Vậy \(EC\perp BH.\)
b. Ta thấy \(O_1\) là trung điểm EB. Vậy thì O1I là đường trung bình của tam giác BEC hay O1I // EC. Tương tự O2I // BH.
Lại có \(EC\perp BH\) nên \(O_1I\perp O_2I.\)
Vậy tam giác O1O2I là tam giác vuông tại I.