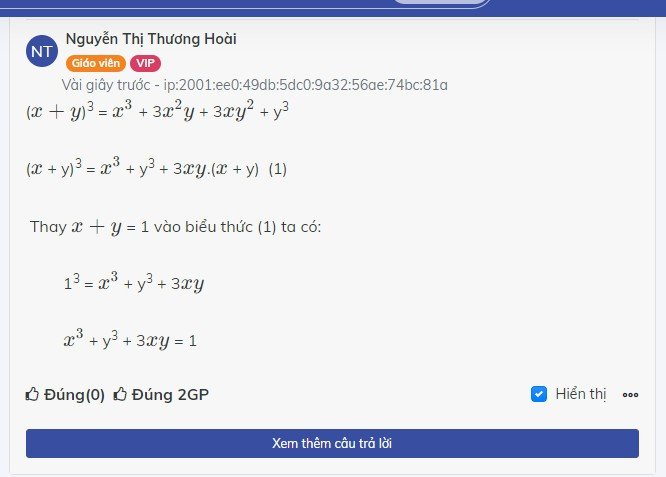
Cho x,y thoả mãn x+y=1. tính giá trị biểu thức x^3+y^3+3xy

Những câu hỏi liên quan
cho hai số thực x,y, thoả mãn x3-3xy2=10 và y3-3x2y=30
tính giá trị biểu thức P=x2+y2
Cho x,y thỏa mãn x+y=1
Tính giá trị biểu thức x^3+y^3+3xy
X3 + Y3 = X3 + 3X2Y + 3 XY2+ Y2+ 3XY - 3 X2Y- 3XY2
=(x + y )3 + 3xy. ( 1 - x - y )
=( x + y)3 + 3xy . [ 1 - (x - y) ]
= 13 + 3xy. ( 1-1)
=1
mik cũng ko chắc nữa nhé
Đúng 0
Bình luận (0)
Ta có :x3 +y3 +3xy=(x+y)(x2 -xy+y2)+3xy
mà x+y=1
=>x2 -xy+y2+3xy=x2 +2xy+y2 =(x+y)2=12 =1
Đúng 0
Bình luận (0)
Giúp em giải hai bài toán này với ạ. Em cảm ơn nhiều ạ
1. Rút gọn biểu thức sau
P= 2. (x+y) (x-y) -(x-y)^2 + (x+y)^2 - 4y^2
2. Cho x, y là 2 số khác nhau thoả mãn x^2 – y = y^2 – x. Tính giá trị của biểu thức A = x^3 + y^3 + 3xy ( x^2+ y^2) 6x^2y^2 ( x+y )
\(1,P=\left(x+y+x-y\right)\left(x+y-x+y\right)+2\left(x^2-y^2\right)-4y^2\\ P=4xy+2x^2-6y^2\)
Đúng 2
Bình luận (0)
Bài 1:
\(P=2\left(x+y\right)\left(x-y\right)-\left(x-y\right)^2+\left(x+y\right)^2-4y^2\)
\(=2\left(x^2-y^2\right)-\left(x^2-2xy+y^2\right)+\left(x^2+2xy+y^2\right)-4y^2\)
\(=2x^2-2y^2-x^2+2xy-y^2+x^2+2xy+y^2-4y^2\)
\(=2x^2+4xy-7y^2\)
Đúng 0
Bình luận (0)
Cho x,y thõa mãn x+y=1.Tính giá trị biểu thức P=x3+3xy+y3
\(P=x^3+3xy+y^3=x^3+3xy\left(x+y\right)+y^3=\left(x+y\right)^3=1^3=1\)
Đúng 0
Bình luận (0)
Cho x, y là 2 số khác nhau thoả mãn x2 – y = y2 – x. Tính giá trị của biểu thức A = x3 + y3 + 3xy(x2 + y2) + 6x2y2(x + y).
Đăng bài lên để nhờ mọi người giải hộ mà không thấy ai giải hộ cả. Giờ mình cũng đã tìm ra cách giải rồi (không biết có đúng không)
* Theo đề bài ra ta có:
x^2 - y = y^2 - x <=> x^2 - y^2 = y - x <=> (x - y)*(x + y) = y - x <=> x + y = (y - x)/(x - y) (điều kiện x - y # 0)
<=> x + y = -(y - x)/(y - x) = -1 (điều kiện x # y).
<=> x = -y. Ta có 2 trường hợp xảy ra:
T/h1: x = y, khi đó A = x^3 + x^3 + 3x*x(x^2 + x^2) + 6x^2*x^2(x + x) = 2x^3 + 3x^2 * 2x^2 + 6x^4 * 2x = 2x^3 + 6x^4 + 12x^5;
T/h2: x =-y, khi đó A = x^3 + (-x)^3 + 3x*(-x)(x^2 + (-x)^2) + 6x^2*(-x)^2(x + (-x))
= x^3 - x^3 - 3x^2(x^2 + x^2) + 6x^2*x^2(x - x) = -6x^4 + 6x^4 * 0 = -6x^4
Đúng 0
Bình luận (0)
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1
Đúng 0
Bình luận (0)
Cho x+y=1 .tính giá trị biểu thức x3 + y3 +3xy và x-y=1 .Tính giá trị biểu thức x3 - y3-3xy
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
Đúng 0
Bình luận (0)
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
a)Cho x+y=1.Tính giá trị của biểu thức x3+y3+3xy
b)Cho x-y=1.Tính giá trị của biểu thức x3-y3-3xy
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Đúng 0
Bình luận (0)
a) cho x + y = 1 . tính giá trị biểu thức x3 + y3 + 3xy
b) cho x-y= 1. tính giá trị của biểu thức x3 - y3 - 3xy
a) \(x+y=1\)
=> \(\left(x+y\right)^3=1\)
<=> \(x^3+y^3+3xy\left(x+y\right)=1\)
<=> \(x^3+y^3+3xy=1\)
b) \(x-y=1\)
=> \(\left(x-y\right)^3=1\)
<=> \(x^3-y^3-3xy\left(x-y\right)=1\)
<=> \(x^3-y^3-3xy=1\)
Đúng 0
Bình luận (0)