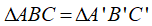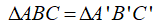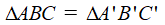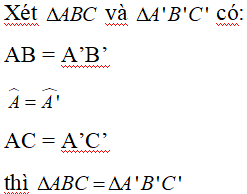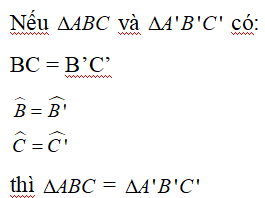3:

=3,45(123+4-27)

=3,45*100=345

2:

a: thể tích của bể là;

18*12*15=3240 lít

b: Hiện tại bể đang chứa:

3240*0,5=1620 lít

4: Đặt \(x=\dfrac{a+b}{a-b};y=\dfrac{b+c}{b-c};z=\dfrac{c+a}{c-a}\).

Ta có \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\dfrac{2a.2b.2c}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)

\(\Rightarrow xy+yz+zx=-1\).

Bất đẳng thức đã cho tương đương:

\(x^2+y^2+z^2\ge2\Leftrightarrow\left(x+y+z\right)^2-2\left(xy+yz+zx\right)-2\ge0\Leftrightarrow\left(x+y+z\right)^2\ge0\) (luôn đúng).

Vậy ta có đpcm

mình xí câu 45,47,51 :>

45. a) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{a}+\dfrac{4}{2b}\ge\dfrac{\left(1+2\right)^2}{a+2b}=\dfrac{9}{a+2b}\left(đpcm\right)\)

Đẳng thức xảy ra <=> a=b

b) Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}\ge\dfrac{\left(1+1+1\right)^2}{a+b+b}=\dfrac{9}{a+2b}\)(1)

\(\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{b+c+c}=\dfrac{9}{b+2c}\)(2)

\(\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{a}\ge\dfrac{\left(1+1+1\right)^2}{c+a+a}=\dfrac{9}{c+2a}\)(3)

Cộng (1),(2),(3) theo vế ta có đpcm

Đẳng thức xảy ra <=> a=b=c

47. Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có :

\(\dfrac{\left(a+b\right)^2}{c}+\dfrac{\left(b+c\right)^2}{a}+\dfrac{\left(c+a\right)^2}{b}\ge\dfrac{\left(a+b+b+c+c+a\right)^2}{a+b+c}=\dfrac{\left[2\left(a+b+c\right)\right]^2}{a+b+c}=\dfrac{4\left(a+b+c\right)^2}{a+b+c}=4\left(a+b+c\right)\)(đpcm)

Đẳng thức xảy ra <=> a=b=c

1. Định nghĩa hai tam giác bằng nhau

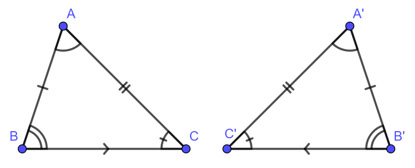
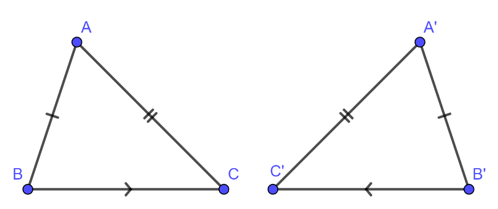
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết :

2. Các trường hợp bằng nhau của tam giác vuông

• Hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )

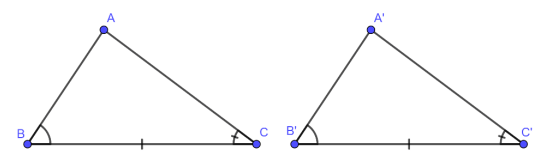
• Cạnh góc vuông và góc nhọn kề cạnh đó

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )

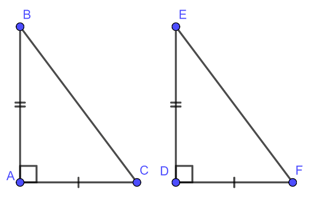
• Cạnh huyền – góc nhọn

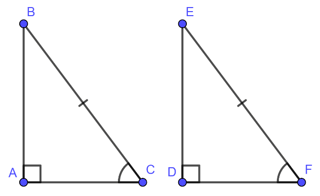
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)

• Cạnh huyền – cạnh góc vuông

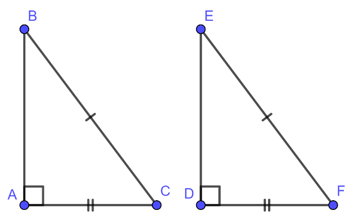
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

1. Định nghĩa hai tam giác bằng nhau

Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C’ ta viết : 

2. Các trường hợp bằng nhau của tam giác

a. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh (c.c.c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Xét 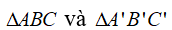 có:

AB = A’B’

AC = A’C’

BC = B’C’

thì 

b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c) 

b. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh (c.g.c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau

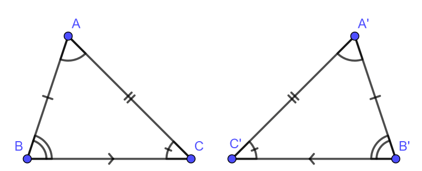
c. Trường hợp bằng nhau thứ ba của hai tam giác: góc – cạnh – góc

Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.

tik cho mình nha mình đc câu1 nè

51 were

52 is going to rain

53 was studying - was chatting

54 does - move

55 were - climbed

56 has - is eating

57 do

58 will come

59 swim

60 has learned - am reading

1 read - cooked 

2 are

3 am going to visit

4 was 

5 ate - was

6 are you going to do - went

a) Xét ΔAEN có 

D là trung điểm của AE

DM//EN

Do đó: M là trung điểm của AN

b) Hình thang DMCB có 

E là trung điểm của DB

EN//DM//CB

Do đó: N là trung điểm của MC

Suy ra: MN=NC

mà MN=AM

nên AM=MN=NC

c) Xét hình thang DMCB có 

E là trung điểm của DB

N là trung điểm của MC

Do đó: EN là đường trung bình của hình thang DMCB

Suy ra: \(EN=\dfrac{DM+CB}{2}\)

hay \(2EN=DM+BC\)

a/ Xét △AEN có:

- \(DM\text{//}EN\left(gt\right)\)

- D là trung điểm của AE \(\left(AD=AE\right)\)

=> DM là đường trung bình của △AEN. Vậy: M là trung điểm của AN (đpcm)

b/ Tứ giác BDMC có \(EN\text{ // }BC\left(gt\right)\) => Tứ giác BDMC là hình thang

 Hình thang BDMC có:

- \(EN\text{ // }BC\left(gt\right)\)

- E là trung điểm của DB \(\left(DE=EB\right)\)

=> EN là đường trung bình của hình thang BDMC => N là trung điểm của MC hay \(MN=NC\)

- Mà \(AM=MN\left(cmt\right)\)

Vậy: \(AM=MN=NC\left(đpcm\right)\)

c/ - Ta có: EN là đường trung bình của hình thang BDMC (cmt)

=> \(EN=\dfrac{DM+BC}{2}\)

Vậy: \(2EN=2\cdot\dfrac{DN+BC}{2}=DN+BC\left(đpcm\right)\)

Số học sinh lớp 3B là:

36 + 4 = 40 (học sinh)

Cả 2 lớp có:

36 + 40 = 76 (học sinh)

Số học sinh lớp 3B là:

       36 + 4 = 40 (học sinh)

Số học sinh của cả 2 lớp là:

       36 + 40 = 76 (học sinh)

                   Đ/S: 76 học sinh 

bn ơi bài 7 mk chẳng thấy tia Cz nằm đâu cả

người đó đến lúc : 11 giờ nha

đến b lúc:

7h45p+2h50p-25=10h10p

SAI THÌ MK SR NHA^^

chị Tâm phải cộng cả thời gian dừng nữa

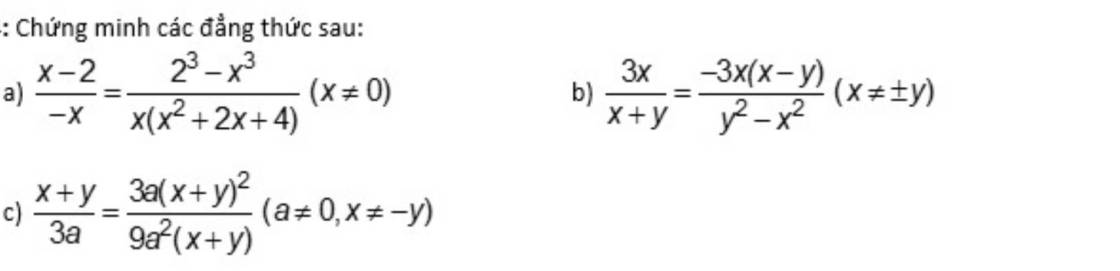
a, \(\dfrac{2^3-x^3}{x\left(x^2+2x+4\right)}\) = \(\dfrac{\left(2-x\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}\) = \(\dfrac{2-x}{x}\)=\(\dfrac{x-2}{-x}\)(đpcm)

b, \(\dfrac{-3x\left(x-y\right)}{y^2-x^2}\) (\(x\) \(\ne\) \(\pm\) y)

= \(\dfrac{-3x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)

= \(\dfrac{3x\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}\)

= \(\dfrac{3x}{x+y}\) (đpcm)

c, \(\dfrac{3a\left(x+y\right)^2}{9a^2\left(x+y\right)}\) (đk a \(\ne\)0; \(x\) \(\ne\) - y)

   = \(\dfrac{3.a.\left(x+y\right)\left(x+y\right)}{3.3.a.a.\left(x+y\right)}\)

   =    \(\dfrac{x+y}{3a}\) (đpcm)