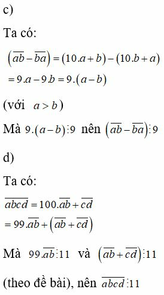Cho ba số tự nhiên a, b, c\(\ne0\). Chứng tỏ rằng: Nếu a là bội của b; b là bội của c thì a là bội của c.

Những câu hỏi liên quan
Cho ba số tự nhiên a,b,c khác 0 , Chứng tỏ rằng : Nếu "a" là bội của "b" , "b" là bội của "c" thì "a" là bội của "c"?
a là bội của b
=> a chia hết cho b
=> a = bk
Mà b chia hết cho c
=> b = cq
=> a = bk = cq.k chia hết cho c
=> a chia hết cho c
=> a là bội của c
=> Đpcm
Đúng 0
Bình luận (0)
cho 3 số tự nhiên a,b,c khác 0 chứng tỏ rằng nếu a là bội của b; b là bội của c thì a là bội của c
a là bội của b => a = b.q ( q là số tự nhiên khác 0) (1)
b là bôị của c => b = c.t ( t là số tự nhiên khác 0) (2)
Thay (2) vào (1) ta có: a = c.t.q => a chia hết cho c
=> a là bội của c (đpcm)
Đúng 0
Bình luận (0)
Theo đề bài
a=m.b (m là số nguyên)
b=n.c (n số nguyên)
=> a=m.n.c
Do m,n là số nguyên => m.n là số nguyên => a là bội của c
Đúng 0
Bình luận (0)
a)Tổng của ba số tự nhiên liên tiếp có chia hết cho 3?
b) chứng tỏ rằng tích của hai số tự nhiên liên tiếp có chia hết cho 2
c) Chứng tỏ rằng mọi số tự nhiên có ba chữ số giống nhau đều là bội của 37.
d) chứng tỏ rằng tổng ab + ba chia hết cho 11
a, gọi 3 số tự nhiên liên tiếp đó là : a; a + 1; a + 2
tổng của chúng là :
a + a + 1 + a + 2
= (a + a + a) + (1 + 2)
= 3a + 3
= 3(a + 1) ⋮ 3 (đpcm)
b, trong 2 số tự nhiên liên tiếp chắc chắn có 1 số chia hết cho 2
=> tích của chúng chia hết chô 2 (đpcm)
c, gọi số tự nhiên có 3 chữ số giống nhau là : aaa (a là chữ số)
aaa = a.111 = a.3.37 ⋮ 37 (đpcm)
d, ab + ba
= 10a + b + 10b + a
= (10a + a) + (10b + b)
= 11a + 11b
= 11(a + b) ⋮ 11 (đpcm)
Đúng 0
Bình luận (0)
d, ab + ba
= 10a + b + 10b + a
= a ( 10 + 1) + b(10+1)
= a.11 + b.11
= ( a + b ).11 \(⋮\)11
Vậy ab + ba \(⋮\)11
Hok tốt
Đúng 0
Bình luận (0)
c,
Gọi số có 3 chữ số giống nhau là aaa ( a\(\inℕ^∗\))
Ta có:
aaa = 111.a = 3.37.a \(⋮\)37 ( đpcm )
Hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
chứng tỏ rằng:a) Tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.b) Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.c)
a
b
¯
-
b
a
¯
⋮
9
(với
a
b
)d) Nếu
a
b...
Đọc tiếp
chứng tỏ rằng:
a) Tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.
b) Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.
c) a b ¯ - b a ¯ ⋮ 9 (với a > b )
d) Nếu a b ¯ + c d ¯ ⋮ 11 thì a b c d ¯ ⋮ 11
1) Cho ba số tự nhiên a,b,c khác 0. Chứng minh rằng: Nếu a là bội của b; b là bội của c thì a là bội của c
2) Tìm x biết: 1+2+3+4+...+x= 3570
3) a/ Tìm hai số tự nhiên liên tiếp có tích bằng 630
b/ Tìm ba số tự nhiên có tích bằng 2184
c/ Tìm hai số tự nhiên liên tiếp bằng 756
d/ Tìm ba số lẻ liên tiếp có tích bằng 1287
Cho 3 số tự nhiên a,b,c khác 0
Chứng tỏ rằng :nếu a là bội của b;b là bội của c thì a là bội của c
Theo bài ta có :
\(a\) là \(B\left(b\right)\) \(\Leftrightarrow a=b.q\left(q\in Z\right)\left(1\right)\)
\(b\) là \(B\left(c\right)\) \(\Leftrightarrow b=c.q_1\left(q_1\in N\right)\left(2\right)\)
Thay \(\left(2\right)\) vào \(\left(1\right)\) ta có :
\(a=c.q.q_1\)
\(\Leftrightarrow a⋮c\)
\(\Leftrightarrow a\) là \(B\left(c\right)\)
\(\Leftrightarrowđpcm\)
Đúng 0
Bình luận (38)
Bài 37: Cho hai số tự nhiên a và b thõa mãn số m = (16a + 17b)(17a + 16b) là một bội số của 11. Chứng tỏ rằng
số m cũng là một bội số của 121.
Xem chi tiết
Chứng tỏ rằng:a, Tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.b, Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.c,
a
b
-
b
a
⋮
9
với abd, Nếu
a...
Đọc tiếp
Chứng tỏ rằng:
a, Tổng của ba số tự nhiên liên tiếp là một số chia hết cho 3.
b, Tổng của bốn số tự nhiên liên tiếp là một số không chia hết cho 4.
c, a b - b a ⋮ 9 với a>b
d, Nếu a b + c d ⋮ 11 thì a b c d ⋮ 11
a, Gọi ba số tự nhiên liên tiếp là: a; a+1; a+2 tổng của ba số này bằng: a+a+1+a+2 = 3a + 3 = 3(a+1) là một số chia hết cho 3.
b, Gọi bốn số tự nhiên liên tiếp là: a; a+1; a+2; a+3 tổng của bốn số này bằng: a+a+1+a+2+a+3 = 4a+6, là một số chia không hết cho 4 vì 4a ⋮ 4 và 6 không chia hết cho 4
c, Ta có: a b - b a = 10 a + b - 10 b + a = 9a - 9b = 9(a - b) với a > b
Mà 9(a - b) ⋮ 9 nên a b - b a ⋮ 9
d, Ta có: a b c d = 100 a b + c d = 99 a b + a b + c d
Mà 99 a b ⋮ 11 và a b + c d ⋮ 11 (đề bài), nên a b c d ⋮ 11
Đúng 0
Bình luận (0)
chứng tỏ rằng : nếu a là bội của b ; b là bội của c thì a là bội của c
a vừa là ước vừa là bội của b thì chắc chắn |a|=b hay a=b hoặc a=-b
có thể chứng minh đơn giản như sau: giả sử a= bx và b=ay ( với x ; y là 2 số nguyên)
thế b=ay vào a=bx ta được: a= axy => xy=1 vì x và y nguyên nên
x=1 và y=1 hoặc x=-1 và y=-1 thay x và y vào điều giả sử ta được a=b hoặc a=-b
Đúng 0
Bình luận (0)
Xem thêm câu trả lời