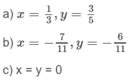Tìm các số nguyên x,y thỏa mãn \(2x^2+4x=19-3y^2\)

Những câu hỏi liên quan
Tìm các số nguyên x,y,z thỏa mãn:2x^2+4x=19-3y^2
Tìm các số nguyên dương x , y thỏa mãn :
\(x^2-6xy+13y^2=100\)
\(2x^2+4x=19-3y^2\)
Tìm các số nguyên x, y thỏa mãn 2x + 3y =19 và \(\dfrac{1}{3}\) < \(\dfrac{x}{y}\)< \(\dfrac{1}{2}\)
\(\dfrac{1}{3}< \dfrac{x}{y}< \dfrac{1}{2}\Rightarrow\dfrac{4}{12}< \dfrac{x}{y}< \dfrac{6}{12}\Rightarrow\dfrac{x}{y}=\dfrac{5}{12}\Rightarrow\dfrac{x}{5}=\dfrac{y}{12}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{12}=\dfrac{2x}{10}=\dfrac{3y}{36}=\dfrac{2x+3y}{10+36}=\dfrac{19}{46}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{95}{46}\\y=\dfrac{114}{23}\end{matrix}\right.\)
Mà \(x,y\in Z\)
Vậy ko có x,y nguyên thỏa mãn đề
Đúng 2
Bình luận (0)
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 1: Tìm các số nguyên x,y thỏa mãn xy+2x-3y=1
Bài 2: Tìm các số nguyên dương x,y,z thỏa mãn (x+1)(y+z)=xyz+2
Bài 4. Tìm các số nguyên x và y thỏa mãn (x+1).( y-2) =5 Bài 5. Tìm các số nguyên x và y thỏa mãn xy -2x + 3y
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
Đúng 1
Bình luận (0)
Số cặp số nguyên \(\left(x;y\right)\)thỏa mãn \(2x^2+3y^2+4x=19\)là ?
2x2 + 3y2 + 4x =19
<=> 2(x+1)2 + 3y2 = 21
=> 3y2 =< 21 <=> y2 =< 7 => y= { -2;-1:0:1:2}
Với y= -2 thì x ko co nghiệm nguyênVới y= -1 thì x có ngiệm là -4 hoặc 2Với y = 0 thì x ko có ngiệm nguyênVới y = 1 thì x có nghiệm là -4 hoặc 2Với y =2 thì x ko có ngiện nguyên Vậy có 4 cặp nghiệm nguyên (x,y) là (-4;-1),(2:-1),(-4:1),(2:1)
Đúng 0
Bình luận (0)
a)tìm các cặp số nguyên dương x,y thỏa mãn: 2x^2+3y^2-5xy-x+3y-4=0
b) các số x,y,z thỏa mãn điều kiện x^2+y^2+z^2=2014. tìm giá trị nhỏ nhất của M=2xy-yz-xz
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i