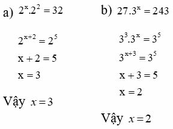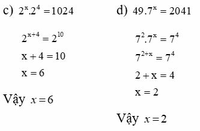a) \(2^{2x}.2^4=1024\)

\(2^{2x}=1024:2^4\)

\(2^{2x}=1024:16\)

\(2^{2x}=64\)

\(2^{2x}=2^6\)

\(\Rightarrow2x=6\)

\(\Rightarrow x=3\)

vay \(x=3\)

b) \(2.3^x=10.3^{12}+8.27^4\)

\(2.3^x=2.5.3^{12}+2^3.\left(3^3\right)^4\)

\(2.3^x=2.5.3^{12}+2^3.3^{12}\)

\(2.3^x=2.3^{12}.\left(5+2^2\right)\)

\(2.3^x=2.3^{12}.9\)

\(2.3^x=2.3^{12}.3^2\)

\(2.3^x=2.3^{14}\)

\(\Rightarrow x=14\)

vay \(x=14\)

c) \(5^8.25^x+1=5^{17}\)

\(5^8.\left(5^2\right)^x+1=5^{17}\)

\(5^8.5^{2x}+1=5^{17}\)

\(5^{8+2x}=5^{17}-1\)

e) \(\left(2x-4\right)^5=\left(2x-4\right)^3\)

\(\left(2x-4\right)^5-\left(2x-4\right)^3=0\)

\(\left(2x-4\right)\left[\left(2x-4\right)^2-1\right]=0\)

\(\left(2x-4\right)\left(2x-4-1\right)\left(2x-4+1\right)=0\)

\(\left(2x-4\right)\left(2x-5\right)\left(2x-3\right)=0\)

\(\Rightarrow2x-4=0\)hoac  \(\orbr{\begin{cases}2x-5=0\\2x-3=0\end{cases}}\)

\(\Rightarrow2x=4\)hoac \(\orbr{\begin{cases}2x=5\\2x=3\end{cases}}\)

 \(\Rightarrow x=2\)hoac \(\orbr{\begin{cases}x=\frac{5}{2}\\x=\frac{3}{2}\end{cases}}\)

              vay \(x=2\)hoac \(\orbr{\begin{cases}x=\frac{5}{2}\\x=\frac{3}{2}\end{cases}}\)

`<=>2^x=1024/162=512/81`

Vì `x\inNN` nên không tồn tại `x` thoả mãn.

Vậy không tồn tại `x` là số tự nhiên thoả mãn đề.

\(\Leftrightarrow2^x=\dfrac{512}{51}\\ \Leftrightarrow x=\log_2\dfrac{512}{51}\)

Mình thấy đề bạn để lớp 6, nhưng lớp 6 thì chưa có học phần này, nên bạn kiểm tra lại đề nhé.

Tách ?

`a, 70 -5.(x-3) =45`

`=> 5.(x-3)= 70-45`

`=> 5.(x-3)=25`

`=>x-3=25:5`

`=>x-3=5`

`=>x= 5+3`

`=>x=8`

______

`b,10 + 2.x = 4^5:4^3`

`=> 10 + 2.x = 4^(5-3)`

`=> 10 + 2.x =4^2=16`

`=> 2.x=16-10`

`=>2.x=6`

`=>x=6:2`

`=>x=3`

_____

`c,60-3.x-2=51`

`=>  60-3.x= 51+2`

`=> 60-3.x=53`

`=>3.x=60-53`

`=> 3.x= 7`

`=>x= 7/3`

____

`d, 4.x-20=2^5:2^3`

`=> 4.x-20=2^(5-3)`

`=> 4.x-20=2^2`

`=> 4.x= 4+20`

`=>4.x=24`

`=>x=24:4`

`=>x=6`

____

`2^x . 4=16`

`=> 2^x=16:4`

`=>2^x= 4`

`=>2^x=2^2`

`=>x=2`

____

`f, 3^x . 3=243`

`=>3^x=243:3`

`=> 3^x=81`

`=> 3^x=3^3`

`=>x=3`

_____

`g, 64. 4^x =16^8`

`=> 4^3 . 4^x=(4^2)^8`

`=> 4^3 . 4^x = 4^(16)`

`=> 4^x= 4^(16-3)`

`=>4^x=4^(13)`

`=>x=13`

_____

`2^x . 16^2 =1024`

`=> 2^x= 1024 : 16^2`

`=>2^x=4`

`=>2^x=2^2`

`=>x=2`

a: =>5(x-3)=25

=>x-3=5

=>x=8

b: =>2x=16-10=6

=>x=3

c: =>58-3x=51

=>3x=7

=>x=7/3

d: =>4x-20=4

=>4x=24

=>x=6

e: =>2^x=4

=>2^x=2^2

=>x=2

f: =>3^x=81

=>3^x=3^4

=>x=4

g: =>4^x*4^3=4^16

=>x+3=16

=>x=13

h: =>2^x=1024/256=4=2^2

=>x=2

a: \(\Leftrightarrow4^{x-5}\cdot17=68\)

=>4^x-5=4

=>x-5=1

=>x=6

b: \(\Leftrightarrow\dfrac{1}{3}:\left|2x-1\right|=\dfrac{1}{3}+\dfrac{2}{3}=1\)

=>|2x-1|=1/3

=>2x-1=1/3 hoặc 2x-1=-1/3

=>x=2/3 hoặc x=1/3

c: =>|2x-2|=|3x+15|

=>3x+15=2x-2 hoặc 3x+15=-2x+2

=>x=-17 hoặc x=-13/5

\(a,|2x-2019|=1\)

\(\Leftrightarrow\orbr{\begin{cases}2x-2019=1\\2x-2019=-1\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}2x=2020\\2x=2018\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=1010\\x=1009\end{cases}}\)

Vậy ............

\(b,\left(2-x\right)^5=-32\)

\(\Leftrightarrow\left(2-x\right)^5=\left(-2\right)^5\)

\(\Leftrightarrow2-x=-2\)

\(\Leftrightarrow x=4\)

Vậy ..........

`@` `\text {Ans}`

`\downarrow`

`2^x = 16`

`=> 2^x = 2^4`

`=> x = 4`

Vậy, `x = 4.`

____

`2^x*16 = 1024`

`=> 2^x =`\(2^{10}\div2^4\)

`=> 2^x = 2^6`

`=> x = 6`

Vậy, `x = 6`

______

`2^x - 26 = 6`

`=> 2^x = 6 + 26`

`=> 2^x = 32`

`=> 2^x = 2^5`

`=> x = 5`

Vậy, `x = 5`

`3^x*3 = 243`

`=> 3^x * 3 = 3^5`

`=> 3^x = 3^5 \div 3`

`=> 3^x = 3^4`

`=> x = 4`

Vậy, `x = 4.`

Câu đúng là A.1024

a,  2 x . 2 2 = 32

2 x + 2 = 2 5

x + 2 = 5

x = 3

Vậy x = 3

b,  27 . 3 x = 243

3 3 . 3 x = 3 5

3 3 + x = 3 5

x + 3 = 5

x = 2

Vậy x = 2

c,  2 x . 2 4 = 1024

2 x + 4 = 2 10

x + 4 = 10

x = 6

Vậy x = 6

d,  49 . 7 x = 2401

7 2 . 7 x = 7 4

7 2 + x = 7 4

2 + x = 4

x = 2

Vậy x = 2

a: \(\left(\sqrt{3}\right)^x=243\)

=>\(3^{\dfrac{1}{2}\cdot x}=3^5\)

=>\(\dfrac{1}{2}\cdot x=5\)

=>x=10

b: \(0,1^x=1000\)

=>\(\left(\dfrac{1}{10}\right)^x=1000\)

=>\(10^{-x}=10^3\)

=>-x=3

=>x=-3

c: \(\left(0,2\right)^{x+3}< \dfrac{1}{5}\)

=>\(\left(0,2\right)^{x+3}< 0,2\)

=>x+3>1

=>x>-2

d: \(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{5}{3}\right)^2\)

=>\(\left(\dfrac{3}{5}\right)^{2x+1}>\left(\dfrac{3}{5}\right)^{-2}\)

=>2x+1<-2

=>2x<-3

=>\(x< -\dfrac{3}{2}\)

e: \(5^{x-1}+5^{x+2}=3\)

=>\(5^x\cdot\dfrac{1}{5}+5^x\cdot25=3\)

=>\(5^x=\dfrac{3}{25,2}=\dfrac{1}{8,4}=\dfrac{10}{84}=\dfrac{5}{42}\)

=>\(x=log_5\left(\dfrac{5}{42}\right)=1-log_542\)