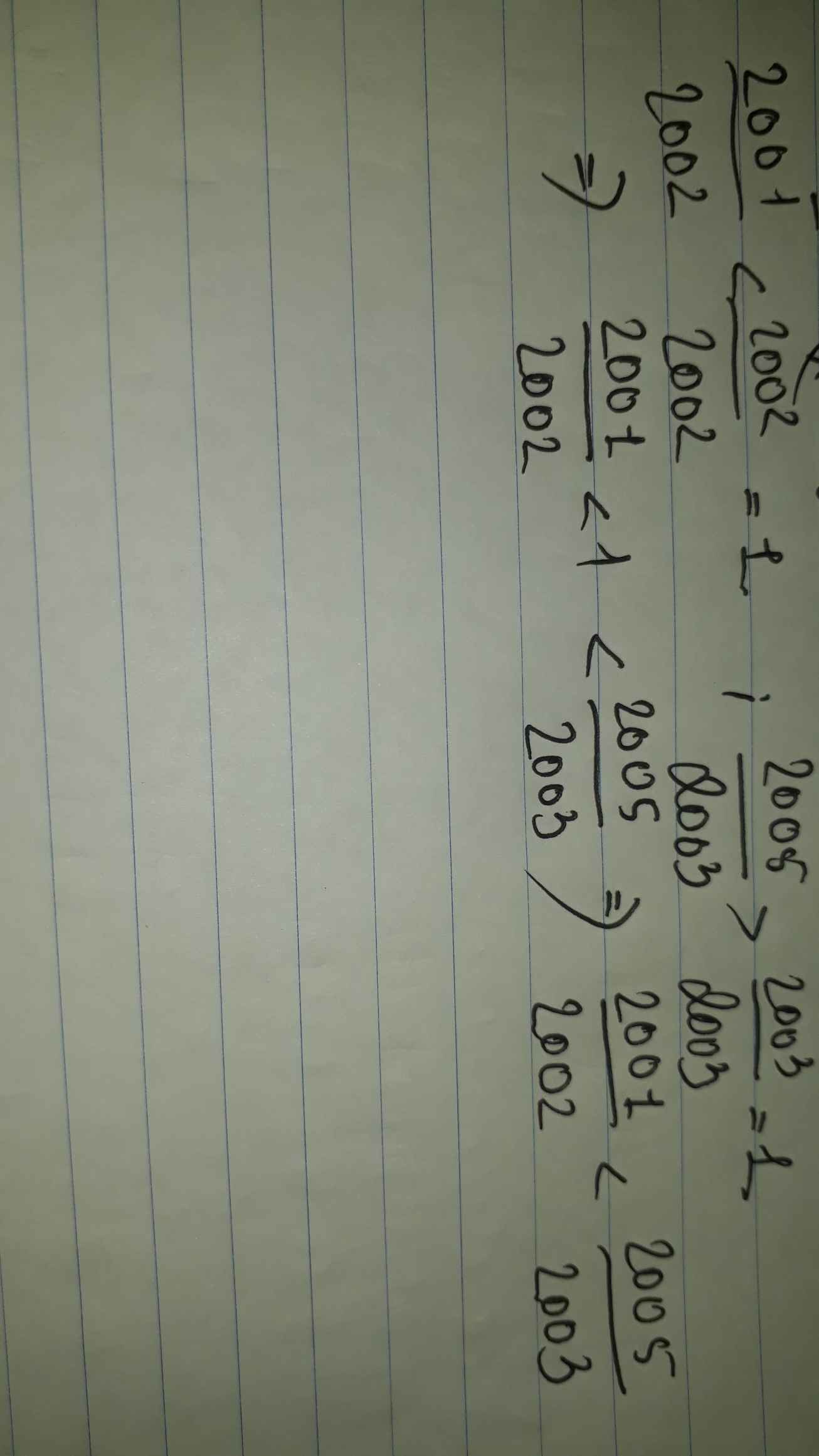so sánh -2005/2010 và 2001/2002

Những câu hỏi liên quan
Cho A = \(\frac{2000}{2001}+\frac{2001}{2002}+\frac{2002}{2003}+\frac{2003}{2004}+\frac{2005}{2006}+\frac{2006}{2007}+\frac{2007}{2008}+\frac{2008}{2009}+\frac{2009}{2010}+\frac{2010}{2011}+\frac{2011}{2012}+\frac{2012}{2013}+\frac{2013}{2014}+\frac{2014}{2015}+\frac{2015}{2016}\)
Hãy so sánh tổng các phân số trong A và so sánh với 15.
mỗi số hạng trong biểu thức A đều nhỏ hơn 1 mà có 15 số nên tổng A sẽ nhỏ hơn 15
Đúng 0
Bình luận (0)
ta thay tong tren <1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
hay tong tren be hon 15
Đúng 0
Bình luận (0)
so sánh các số hữu tỉ 2001/2002 và 2005/2003
ta có\(\dfrac{2001}{2002}< 1\)và\(\dfrac{2005}{2003}>1\)
\(\Rightarrow\dfrac{2001}{2002}< \dfrac{2005}{2003}\)
Đúng 1
Bình luận (0)
Ta có: \(\dfrac{2001}{2002}< 1\)
mà \(1< \dfrac{2005}{2003}\)
nên \(\dfrac{2001}{2002}< \dfrac{2005}{2003}\)
Đúng 0
Bình luận (0)
1/ So sánh các số hữu tỉ sau
a/ \(\frac{13}{17}và\frac{46}{50}\)
b/ \(\frac{33}{131}và\frac{53}{217}\)
c/ \(\frac{41}{91}và\frac{411}{911}\)
d/ \(\frac{2001}{2002}và\frac{2005}{2003}\)
e/ \(\frac{-2005}{2010}và\frac{2001}{2002}\)
a.\(\frac{13}{17}\)=1-\(\frac{4}{17}\); \(\frac{46}{50}\)=1-\(\frac{4}{50}\)
Vì \(\frac{4}{17}\)>\(\frac{4}{50}\)=> 1-\(\frac{4}{17}\)<1-\(\frac{4}{50}\)
Vậy\(\frac{13}{17}\)<\(\frac{46}{50}\)
Đúng 0
Bình luận (0)
c.\(\frac{41}{91}\)=1-\(\frac{50}{91}\)=1-\(\frac{500}{910}\); \(\frac{411}{911}\)=1-\(\frac{500}{911}\)
Vì \(\frac{500}{910}\)>\(\frac{500}{911}\)=>1-\(\frac{500}{910}\)<1-\(\frac{500}{911}\)=>\(\frac{41}{91}\)<\(\frac{411}{911}\)
Đúng 0
Bình luận (0)
d. \(\frac{2001}{2002}< \frac{2002}{2002}=1;\frac{2005}{2003}>\frac{2003}{2003}=1\text{ hay }\frac{2001}{2002}< 1< \frac{2005}{2003}\)
Vậy \(\frac{2001}{2002}< \frac{2005}{2003}\).
e. \(-\frac{2005}{2010}< 0;\frac{2001}{2002}>0\text{ hay }-\frac{2005}{2010}< 0< \frac{2001}{2002}\)
Vậy \(-\frac{2005}{2010}< \frac{2001}{2002}\).
b. \(\frac{33}{131}>\frac{33}{132}=\frac{1}{4};\frac{53}{217}< \frac{53}{212}=\frac{1}{4}\text{ hay }\frac{53}{217}< \frac{1}{4}< \frac{33}{131}\)
Vậy \(\frac{53}{217}< \frac{33}{131}\).
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh
A 2010*2010-1945
2010*2010+65 và
B 2001*2001+111
2001*2002-1890
Ta có
\(A=\frac{2010.2010-1945}{2010.2010+65}
Đúng 0
Bình luận (0)
Cho A=2002/2001+2003/2002+2004/2003+2005/2004+2006/2005+2007/2006+2008/2007+2009/2008
Hãy so sánh A với 8 và giải thích tại sao
2002/2001>:,2003/2002>1.....
CÓ 8 PHÂN SỐ MỖI PHÂN SỐ CÓ GIÁ TRỊ LỚN HƠN 1 VÂY TỔNG CỦA 8 PHÂN SỐ LỚN HƠN 1 SẼ LỚN HƠN 8.
Đúng 0
Bình luận (0)
Cho A =2002/2001+2003/2002+2004/2003+2005/2004+2006/2005+2007/2006+2008/20007+2009/20008.So sánh A với 8
So sánh : a) A = 2001 + 2002 / 2002 + 2003 và B = 2001/2002 + 2002/ 2003
b) A = 2006^2006 + 1/2006^2007 +1 và B = 2006^2005 + 1/2006^2006 + 1
c ) A = 1999^1999 + 1/1999^2000 + 1 và B = 1999^1989 + 1/1999^2009 + 1
B = \(\frac{2001}{2002}+\frac{2002}{2003}\)
có: \(\frac{2000}{2001}>\frac{2000}{2001}+2002\)
\(\frac{2001}{2002}>\frac{2001}{2001}+2002\)
Vậy A>B
Đúng 0
Bình luận (0)
\(B=\frac{2009-\frac{2009}{2001}-\frac{2009}{2002}-\frac{2009}{2003}-\frac{2009}{2004}}{2010-\frac{2010}{2001}-\frac{2010}{2002}-\frac{2010}{2003}-\frac{2010}{2004}}:\frac{2009-\frac{2009}{2005}-\frac{2009}{2006}-\frac{2009}{2007}-\frac{2009}{2008}}{2010-\frac{2010}{2005}-\frac{2010}{2006}-\frac{2010}{2007}-\frac{2010}{2008}}\)
minh lam duoc roi . cach viet phan so ban bam vao o mau vang o cuoi trang .cu di con chuot xuong cuoi trang thi thay 1 o vang , vao xem huong dan la biet ngay ma.
Đúng 0
Bình luận (0)
Trình bày bài giải bài toán sau
Cho A=2002/2001+2003/2002+ 2004/2003+2005/2004+2006/2005+2007/2006+2008/2007+2009/2008
Hãy so sánh A với 8
\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>\frac{2001}{2001}+\frac{2002}{2002}+\frac{2003}{2003}+\frac{2004}{2004}+\frac{2005}{2005}+\frac{2006}{2006}+\frac{2007}{2007}+\frac{2008}{2008}\)
\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>1+1+1+1+1+1+1+1\)\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>8\)
\(A>8\)
Đúng 1
Bình luận (0)