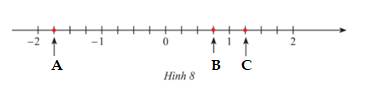
a)      Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)

b)      Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)

Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

-1/3: chia giữa 0 và -1 thành 3 phần lấy 1 phần bên phải gần 0

3/3=1

5/3: chia giữa 1,2 và 3 thành 5 phần : 3 phần giữa 1 và 2, 2 phần giữa 2 và 3, lấy 2 phần ở gần 2

|------|------|------|----|--|------|----|--|------|------|------|----->

                          -1/3 0    3/3 5/3

Mình làm rồi bạn nhé!

a) HS tự biểu diễn. b) Các số nguyên âm gồm có: -4; -3; -2. HS tự biểu diễn. c) Không

a) Biểu diễn các số –3; –4; 2; 4 trên trục số.

b) Ghi các số nguyên âm nằm giữa các số –5 và –1 trên trục số.

c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –5 và –4

cách 1: \(\frac{-3}{5}\)(cách viết dạng phân số)

cách 2:  (-3) : 5 ( cách viết dạng phép chia)

cách 3: -0,6     ( cách viết dạng số thập phân)

a) Ta có: \( - 0,625 = \frac{{ - 625}}{{1000}}= \frac{{ - 625:125}}{{1000:125}} = \frac{{ - 5}}{8}\)

\(\begin{array}{l}\frac{5}{{ - 8}} = \frac{{ - 5}}{8};\\\frac{{10}}{{16}} = \frac{{10:2}}{{16:2}} = \frac{5}{8};\\\frac{{20}}{{ - 32}} = \frac{{20:( - 4)}}{{( - 32):( - 4)}} = \frac{{ - 5}}{8};\\\frac{{ - 10}}{{16}} = \frac{{( - 10):2}}{{16:2}} = \frac{{ - 5}}{8};\\\frac{{ - 25}}{{40}} = \frac{{( - 25):5}}{{40:5}} = \frac{{ - 5}}{8};\\\frac{{35}}{{ - 48}}\end{array}\)

Vậy các phân số biểu diễn số hữu tỉ -0,625 là:

\(\frac{5}{{ - 8}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}}\)

b) Ta có: \( - 0,625 = \frac{{ -5}}{{8}}\) nên ta biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\) trên trục số.

Chia đoạn thẳng đơn vị thành 8 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{8}\) đơn vị cũ.

Lấy một điểm nằm trước O và cách O một đoạn bằng 5 đơn vị mới. Điểm đó biểu diễn số hữu tỉ \(\frac{{ -5}}{{8}}\)

-0,6; \(\frac{-6}{10}\); \(\frac{-9}{15}\)