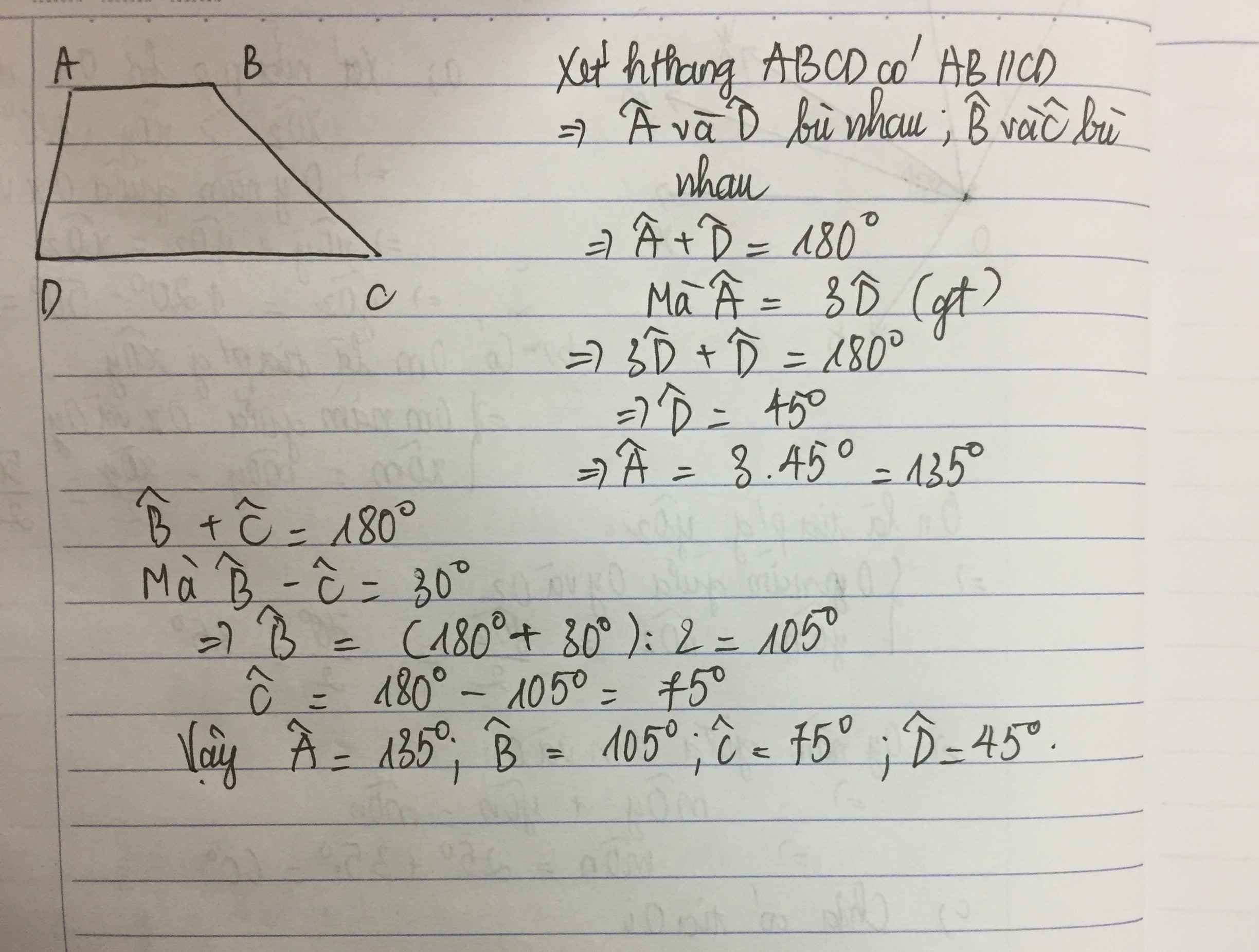Cho hình thang ABCD (AB//CD) . Tính các góc của hình thang biết 2A^=3D^ và C^+20o=B^

Những câu hỏi liên quan
hình thang ABCD (AB// CD) có góc A - góc B = 20o, góc B = 2 góc C. Tính các góc của hình thang.
Ta có: AB//CD
nên \(\widehat{A}+\widehat{B}=180^0\)
\(\Leftrightarrow\widehat{A}=100^0\)
\(\Leftrightarrow\widehat{B}=80^0\)
hay \(\widehat{C}=40^0\)
Ta có: AB//CD
nên \(\widehat{C}+\widehat{D}=180^0\)
\(\Leftrightarrow\widehat{D}=140^0\)
Đúng 1
Bình luận (0)
.cho hình thang ABCD có A^=3D^, B^=C^(AB//CD)
AB=\(\sqrt{2cm}\), AD=3cm,CD=4cm
a)cmr A^+B^=C^+D^
b)tính các góc của hình thang ABCD
c)tính diện tích của hình thang ABCD
a: Xét hình thang ABCD(AB//CD có
\(\widehat{B}=\widehat{C}\)
nên ABCD là hình thang cân
Đúng 0
Bình luận (0)
Tính các góc của hình thang ABCD ( AB // CD ) , biết rằng A= 3D và B - C = 30o
Ta có:
Xét hình thang ABCD(AB//CD) ta có:
\(\widehat{A}+\widehat{D}=\widehat{B}+\widehat{C}=180^0\)
Mà \(\left\{{}\begin{matrix}\widehat{A}=3\widehat{D}\\\widehat{B}-\widehat{C}=30^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3\widehat{D}+\widehat{D}=180^0\\30^0+\widehat{C}+\widehat{C}=180^0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{D}=45^0\\\widehat{C}=75^0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\widehat{A}=135^0\\\widehat{B}=105^0\end{matrix}\right.\)
Vậy...
Đúng 1
Bình luận (0)
Cho hình thang ABCD(AB//CD) CÓ góc A =3D^ GÓC B = góc C AB=3cm CD=4cm TÍNH độ dài đg cao AH của hình thang và diện tích hình thang
Cho hình thang ABCD ( AB//CD) có A=3D, B=C, AB= căn 2 cm, BC=3cm, CD= 4cm
1. CMR: A+D=B+C
2. Tính số đo các góc của hình thang
3. Tính đường cao và S(ABCD)
1: AB//CD
=>góc A+góc D=180 độ và góc B+góc C=180 độ
=>góc A+góc D=góc B+góc C
2: góc A+góc D=180 độ
góc A=3*góc D
=>góc A=3/4*180=135 độ và góc D=180-135=45 độ
góc B=góc C
góc B+góc C=180 độ
=>góc B=góc C=180/2=90 độ
Đúng 0
Bình luận (0)
Tính các góc của hình thang ABCD biết AB // CD, B-C 30 độ ;A=3D
Tính các góc của hình thang ABCD (AB // CD), biết rằng A = 3D, B - C = 30 0
Ta có: hình thang ABCD có AB // CD ⇒ ∠ A + ∠ D = 180 0 (hai góc trong cùng phía)
Ta có: ∠ A = 3 ∠ D (gt)
⇒ 3 ∠ D + ∠ D = 180 0 ⇒ 4 ∠ D = 180 0 ⇒ ∠ D = 45 0 ⇒ ∠ A = 3. 45 0 = 135 0
∠ B + ∠ C = 180 0 (hai góc trong cùng phía)
∠ B - ∠ C = 30 0 (gt)
⇒ 2 ∠ B = 180 0 + 30 0 = 210 0 ⇒ ∠ B = 105 0
∠ C = ∠ B - 30 0 = 105 0 – 30 0 = 75 0
Đúng 2
Bình luận (0)
Tính các góc của hình thang ABCD (AB//CD) , biết rằng A =3D , B- c = 30
theo tính chất của hình thang thì tổng 2 góc kề 2 cạnh bên =180
theo đó: nếu AB,CD là 2 đáy hình thang thì
góc A+góc D=180 <=> D+3D=180 <=> 4D=180 <=> D=45 độ => A=3.45=135
góc B-C=30 => B=C+30
B+C=180<=> C+30+C=180 <=> 2C=150 <=> C=75 độ => B=75+30=105
Đúng 1
Bình luận (0)
cho mot hinh thang AB//CD biet B-C= 30 tinh cac goc con lai
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính các góc của hình thang ABCD (AB//CD), biết rằng góc A = Góc 3D, góc B- góc C =30°
\(\widehat{DAB}+\widehat{ADC}=180^0\)
mà \(\widehat{DAB}=3\widehat{ADC}\)\(\Rightarrow\widehat{ADC}=45^0\Rightarrow\widehat{DAB}=135^0\)
\(\widehat{ABC}+\widehat{BCD}=180^0\) mà lại có: \(\widehat{ABC}-\widehat{BCD}=30^0\)
\(\Rightarrow\widehat{BCD}=75^0\Rightarrow\widehat{ABC}=105^0\)
Đúng 2
Bình luận (0)