Cho hình tháng vuông ABCD có 2 đường chéo AC và DB vuông học với nhau tại H. biết HD= 18cm, Hb=8cm. Tính định tích hình thanh ABCD

Những câu hỏi liên quan
Cho hình thang vuông ABCD (
∠
A
∠
D
90
0
) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD 18cm, HB 8cm, tính diện tích hình thang ABCD A. 504
c
m
2
B. 505
c
m
2
C. 506
c
m
2
D. 506
c
m...
Đọc tiếp
Cho hình thang vuông ABCD ( ∠ A = ∠ D = 90 0 ) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD = 18cm, HB = 8cm, tính diện tích hình thang ABCD
A. 504 c m 2
B. 505 c m 2
C. 506 c m 2
D. 506 c m 2
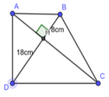
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
bài 1: CHo hình thang vuông ABCD có hai đường chéo Ac và BD vuông góc với nhau tại H. biết HD= 18cm, HB= 8cm. Tính diện tích hình thang ABCD
bài 2:Cho tam giác vuông ABC vuông tại A, đường cao Ah. tính độ dài các đoạn thắng BH,AH,AC nếu biết
a, AB=12cm, Ch=12,8cm
b, AB=4 cm, Ch=2/2 cm
Cho hình thang vuông ABCD (góc A = góc D = 90o ) có AC vuông góc với BD tại H .Biết HB=8cm, HD=18cm .Tính diện tích hình thang
Ta có: \(AH^2=HD.HB=18.8=144\Rightarrow AH=12\) (cm)
\(\Rightarrow AD=\sqrt{AH^2+HD^2}=\sqrt{12^2+18^2}=6\sqrt{13}\)
\(AB=\sqrt{12^2+8^2}=4\sqrt{13}\)
Ta có: \(DH^2=HA.HC\Rightarrow CH=\dfrac{DH^2}{HA}=\dfrac{18^2}{12}=27\)
\(\Rightarrow CD=\sqrt{CH^2+HD^2}=\sqrt{27^2+18^2}=9\sqrt{13}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AD=\dfrac{1}{2}\left(4\sqrt{13}+9\sqrt{13}\right).6\sqrt{13}\)
\(=507\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD vuông tại A và D, 2 đường chéo AC và BD vuông góc với nhau. Biết AB = 18cm, CD = 32cm. Tính AC.
cho hình thang vuông tại A và D, 2 đường chéo AC và DB cắt nhau và vuông góc tại O, biết AB=2√13, OA=6. Tính diện tích hình thang ABCD
Hình thang vuông ABCD có AC vuông góc với BD tại O. Tính diện tích ABCD biết OB=8cm, OD=18cm
Cho hình thang ABCD có góc B= góc C =90o. Hai đường chéo vuông góc với nhau tại H. Biết AB=3 căn 5 cm,HA=3cm.Tinh HB,HC,HD
Bài 2. Cho hình thang ABCD có hai đường chéo AC, DB vuông góc nhau, đường cao BH.Cho BH=12cm,BD=15cm.C Qua B vẽ đường thẳng song song với AC cắt DC tại E.a) Chứng minh: BD^ 2 =DH.DE b) Tính diện tích hình thang ABCD
cho hình vuông abcd có 2 đường chéo ac và bd vuông góc với nhau và bằng 12 cm, 2 đường chéo này cắt nhau tại o. từ o ta vẽ 1 hình tròn có đường kính bằng cạnh hình vuông abcd
tính diện tích hình tròn này














