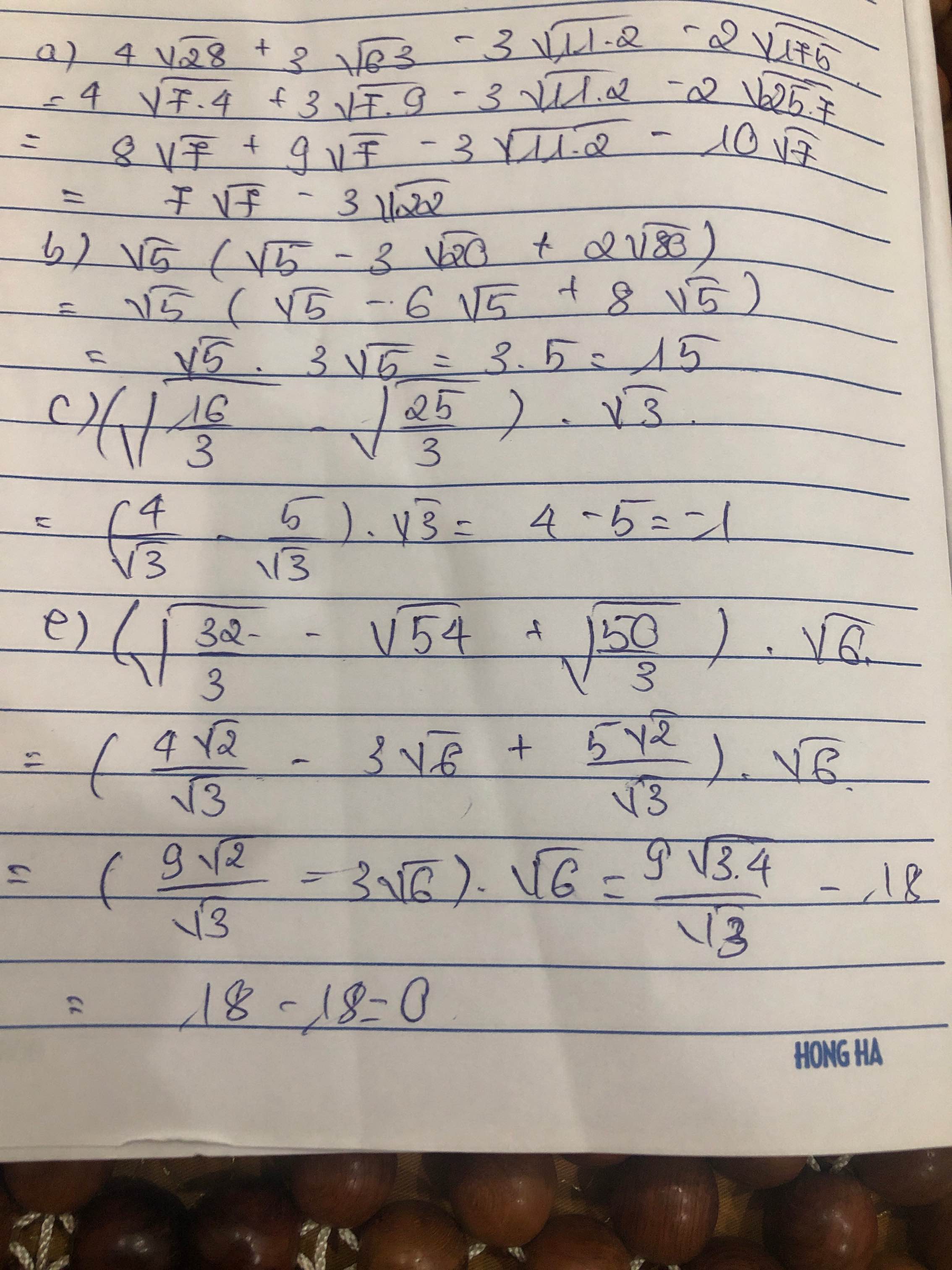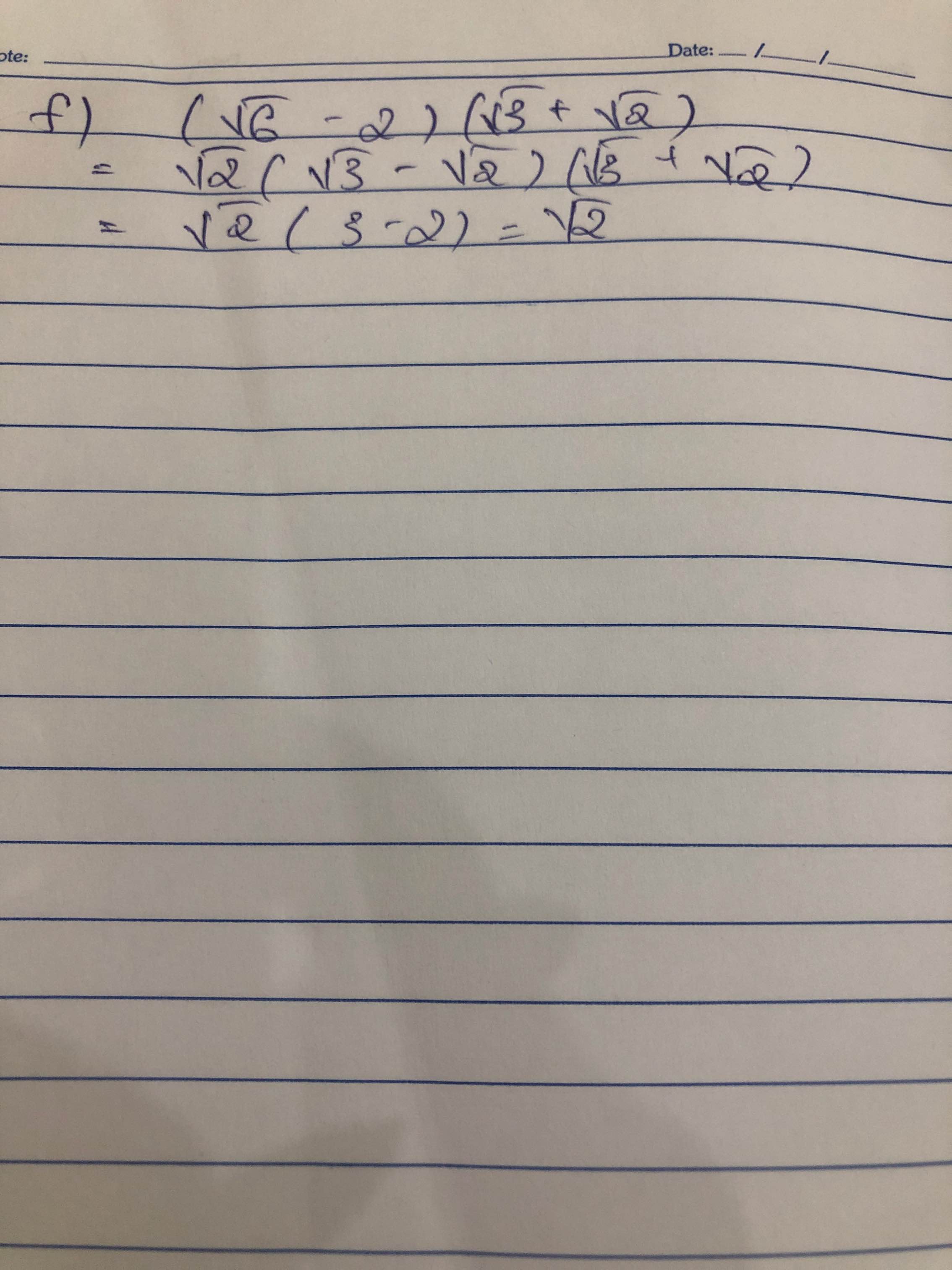Chứng tỏ: \(\sqrt[3]{20}+\sqrt[3]{2}-\sqrt[3]{25}=3\sqrt[3]{\sqrt[3]{5}-\sqrt[3]{4}}\)

Những câu hỏi liên quan
Chứng tỏ: \(\sqrt[3]{20}+\sqrt[3]{2}+\sqrt[3]{25}=3\sqrt[3]{\sqrt[3]{5}-\sqrt[3]{4}}\)
Chứng tỏ :\(\sqrt[3]{20}+\sqrt[3]{2}-\sqrt[3]{2}=3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
Chứng minh \(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}=3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
\(\hept{\begin{cases}\left(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\right)^2=9\left(\sqrt[3]{5}-\sqrt[3]{4}\right)\\\left(3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\right)^2=9\left(\sqrt[3]{5}-\sqrt[3]{4}\right)\end{cases}}\)
Đúng 0
Bình luận (0)
Rút gọn biểu thứcI(2sqrt{3}-5sqrt{27}+4sqrt{12}):sqrt{3}Ksqrt{125}-4sqrt{45}+3sqrt{20}-sqrt{80}L2sqrt{9}+sqrt{25}-5sqrt{4}N2sqrt{32}-5sqrt{27}-4sqrt{8}+3sqrt{75}O2sqrt{3.5^2}-3sqrt{3.2^2}+sqrt{3.3^2}
Đọc tiếp
Rút gọn biểu thức
I=(2\(\sqrt{3}\)-5\(\sqrt{27}\)+4\(\sqrt{12}\)):\(\sqrt{3}\)
K=\(\sqrt{125}\)-4\(\sqrt{45}\)+3\(\sqrt{20}\)-\(\sqrt{80}\)
L=2\(\sqrt{9}\)+\(\sqrt{25}\)-5\(\sqrt{4}\)
N=2\(\sqrt{32}\)-5\(\sqrt{27}\)-4\(\sqrt{8}\)+3\(\sqrt{75}\)
O=2\(\sqrt{3.5^2}\)-3\(\sqrt{3.2^2}\)+\(\sqrt{3.3^2}\)
\(I=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\sqrt{3}.\sqrt{3^2}+2\sqrt{2^2}.\sqrt{3}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
\(=-5\sqrt{3}.\dfrac{1}{\sqrt{3}}\)
\(=-5\)
\(K=\sqrt{125}-4\sqrt{45}+3\sqrt{20}-\sqrt{80}\)
\(=\sqrt{5^2.5}-4\sqrt{3^2.5}+3\sqrt{2^2.5}-\sqrt{4^2.5}\)
\(=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}\)
\(=\sqrt{5}.\left(5-12+6-4\right)\)
\(=-5\sqrt{5}\)
\(L=2\sqrt{9}+\sqrt{25}-5\sqrt{4}\)
\(=2\sqrt{3^2}+\sqrt{5^2}-5\sqrt{2^2}\)
\(=2.3+5-5.2\)
\(=1\)
\(N=2\sqrt{32}-5\sqrt{27}-4\sqrt{8}+3\sqrt{75}\)
\(=2.4\sqrt{2}-5.3\sqrt{3}-4.2\sqrt{2}+3.5\sqrt{3}\)
\(=8\sqrt{2}-8\sqrt{2}-15\sqrt{3}+15\sqrt{3}\)
\(=0\)
\(O=2\sqrt{3.5^2}-3\sqrt{3.2^2}+\sqrt{3.3^2}\)
\(=2.5\sqrt{3}-3.2\sqrt{3}+3\sqrt{3}\)
\(=10\sqrt{3}-6\sqrt{3}+3\sqrt{3}\)
\(=7\sqrt{3}\)
Đúng 3
Bình luận (0)
\(L=\dfrac{2\sqrt{3}-15\sqrt{3}+8\sqrt{3}}{\sqrt{3}}=2-15+8=-5\)
\(K=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}=-5\sqrt{5}\)
L=2*3+5-5*2=5-4=1
N=8căn 2-8căn2-15căn3+15căn 3=0
O=10căn 3-6căn3+3căn3=7căn 3
Đúng 2
Bình luận (0)
bài 2a) 4sqrt{28}+3sqrt{63}-3sqrt{11.2}-2sqrt{175}b) sqrt{5}.left(sqrt{5}-3sqrt{20}+2sqrt{80}right)c) left(sqrt{dfrac{16}{3}}-sqrt{dfrac{25}{3}}right).sqrt{3}e) left(sqrt{dfrac{32}{3}}-sqrt{54}+sqrt{dfrac{50}{3}}right).sqrt{6}f) left(sqrt{6}-2right).left(sqrt{3}+sqrt{2}right)
Đọc tiếp
bài 2
a) \(4\sqrt{28}+3\sqrt{63}-3\sqrt{11.2}-2\sqrt{175}\)
b) \(\sqrt{5}.\left(\sqrt{5}-3\sqrt{20}+2\sqrt{80}\right)\)
c) \(\left(\sqrt{\dfrac{16}{3}}-\sqrt{\dfrac{25}{3}}\right).\sqrt{3}\)
e) \(\left(\sqrt{\dfrac{32}{3}}-\sqrt{54}+\sqrt{\dfrac{50}{3}}\right).\sqrt{6}\)
f) \(\left(\sqrt{6}-2\right).\left(\sqrt{3}+\sqrt{2}\right)\)
a) Ta có: \(4\sqrt{28}+3\sqrt{63}-3\sqrt{112}-2\sqrt{175}\)
\(=8\sqrt{7}+9\sqrt{7}-12\sqrt{7}-10\sqrt{7}\)
\(=-5\sqrt{7}\)
b) Ta có: \(\sqrt{5}\left(\sqrt{5}-3\sqrt{20}+2\sqrt{80}\right)\)
\(=\sqrt{5}\left(\sqrt{5}-6\sqrt{5}+8\sqrt{5}\right)\)
\(=\sqrt{5}\cdot3\sqrt{5}=15\)
c) Ta có: \(\left(\sqrt{\dfrac{16}{3}}-\sqrt{\dfrac{25}{3}}\right)\cdot\sqrt{3}\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\sqrt{3}\)
=-1
e) Ta có: \(\left(\sqrt{\dfrac{32}{3}}-\sqrt{54}+\sqrt{\dfrac{50}{3}}\right)\cdot\sqrt{6}\)
\(=\left(\dfrac{4\sqrt{2}}{\sqrt{3}}+\dfrac{5\sqrt{2}}{\sqrt{3}}-3\sqrt{6}\right)\cdot\sqrt{6}\)
\(=\dfrac{9\sqrt{12}}{\sqrt{3}}-18\)
\(=0\)
f) Ta có: \(\left(\sqrt{6}-2\right)\left(\sqrt{3}+\sqrt{2}\right)\)
\(=3\sqrt{2}+2\sqrt{3}-2\sqrt{2}-2\sqrt{2}\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (1)
C/ minh N = \(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}=3\sqrt[3]{\sqrt[3]{5}-\sqrt[3]{4}}\)
Chứng minh \(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\)= \(3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
Giúp mình với nha!!!!!! Mình sẽ tick cho các bạn
\(\left(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\right)^2\)
\(=\sqrt[3]{4}+2\sqrt[3]{50}+5\sqrt[3]{5}+2\left(2\sqrt[3]{5}-\sqrt[3]{50}-5\sqrt[3]{4}\right)\)
\(=9\sqrt[3]{5}-9\sqrt[3]{4}=9\left(\sqrt[3]{5}-\sqrt[3]{4}\right)\)
\(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}=3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
Đúng 0
Bình luận (0)
thanks bạn nhiều nha!!!! Chúc bạn hok tốt
Đúng 0
Bình luận (0)
cmr các đẳng thức :
1/\(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}=3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
2/\(\frac{\sqrt[4]{5}+1}{\sqrt[4]{5}-1}=\sqrt[4]{\frac{3+2\sqrt[4]{5}}{3-2\sqrt[4]{5}}}\)
3/\(\sqrt[3]{\sqrt[3]{2}-1}=\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}\)
giúp mik vs mik cần gấp lắm
Tính:
a/ \(\frac{3+\sqrt{5}}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\frac{3-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
b/ \(\frac{\sqrt{20+8\sqrt{3}}+\sqrt{20-8\sqrt{3}}}{\sqrt{5+2\sqrt{3}}-\sqrt{5-2\sqrt{3}}}-\frac{\sqrt{4+\sqrt{3}}+\sqrt{4-\sqrt{3}}}{\$\sqrt{4+\sqrt{3}}-\sqrt{4-\sqrt{3}}}\)