1: góc MAO+góc MBO=180 độ

=>MAOB nội tiếp

2: Xét ΔIBF và ΔIAB có

góc IBF=góc IAB

góc BIF chung

=>ΔIBF đồng dạng với ΔIAB

=>IB/IA=IF/IB

=>IB^2=IA*IF

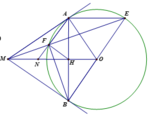
1) Chứng minh: Tứ giác MAOB nội tiếp một đường tròn

Vẽ được các yếu tố để chứng minh phần (1).

Ta có M B O ^ = 90 0 ,   M A O ^ = 90 0  (theo t/c của tiếp tuyến và bán kính)

Suy ra:  M A O ^ + M B O ^ = 180 0 .Vậy tứ giác MAOB nội tiếp đường tròn.

2) Chứng minh: MN² = NF. NA và MN = NH

Ta có A E / / M O ⇒ A E M ^ = E M N ^   mà   A E M ^ = M A F ^ ⇒ E M N ^ = M A F ^

Δ N M F   v à   Δ N A M có:  M N A ^ chung;  E M N ^ = M A F ^

nên  Δ N M F đồng dạng với  Δ N A M

⇒ N M N F = N A N M ⇒ N M 2 = N F . N A        1

Mặt khác có: A B F ^ = A E F ^ ⇒ A B F ^ = E M N   ^ h a y   H B F ^ = F M H ^  

=> MFHB là tứ giác nội tiếp

⇒ F H M ^ = F B M ^ = F A B ^   h a y   F H N ^ = N A H ^

Xét Δ N H F   &   Δ N A H   c ó   A N H   ^ c h u n g ;   N H F ^ = N A H ^

=> Δ N M F đồng dạng  Δ N A H ⇒ ⇒ N H N F = N A N H ⇒ N H 2 = N F . N A        2  

Từ (1) và (2) ta có NH = HM

3) Chứng minh:  H B 2 H F 2 − EF M F = 1 .

Xét Δ M AF  và Δ M E A  có: A M E ^  chung, M A F ^ = M E A ^

suy ra  Δ M AF  đồng dạng với  Δ M E A

⇒ M E M A = M A M F = A E A F ⇒ M E M F = A E 2 A F 2      (3)

Vì MFHB là tứ giác nội tiếp ⇒ M F B ^ = M H B ^ = 90 0 ⇒ B F E ^ = 90 0 và A F H ^ = A H N ^ = 90 0 ⇒ A F E ^   = B F H ^  

Δ A E F  và Δ H B F  có: E F A ^ = B F H ^   ;   F E A ^ = F B A ^

suy ra  Δ A E F   ~   Δ H B F  

⇒ A E A F = H B H F ⇒ A E 2 A F 2 = H B 2 H F 2                (4)

Từ (3) và (4) ta có M E M F = H B 2 H F 2 ⇔ M F + F E M F = H B 2 H F 2 ⇔ 1 + F E M F = H B 2 H F 2 ⇔ H B 2 H F 2 − F E M F = 1

a: góc OBA+góc OCA=180 độ

=>ABOC nội tiếp

Xét (O) có

AB,AC là tiếp tuyến

=>AB=AC
mà OB=OC

nên OA là trung trực của BC

=>OA vuông góc BC

b: DE//CF

=>sđ cung CD+sđ cung EF
góc AIB=1/2(sđ cung BD+sđ cung EF)

ABOC nội tiếp

=>góc AOB=góc ACB=1/2*sđ cung BC

=1/2(sđ cung EF+sđ cung EB)

=>góc AIB=góc AOB

=>AOIB nội tiếp

=>góc OIA=90 độ

ΔODE cân tại O

mà OI là đường cao

nên I là trung điểm của DE

Ta có: \(\widehat{OAM}=\widehat{OBM}=90^o\)(Vì AM là đường trung tuyến của (O))

\(\Rightarrow\widehat{OAM}+\widehat{OBM}=180^o\)

=> Tứ giác MAOB nội tiếp

Theo tính chất tiếp tuyến cắt nhau ta có MA=MB; OA=OB 

=> MO là đường trung trực của AB 

=> MO _|_ AB tại H

Mà \(\widehat{BAE}=90^o\)hay AE _|_ AB. Do đó AE // MO

Vì AE // MO và MA là tiếp tuyến của (O) nên \(\widehat{NMF}=\widehat{AEF}=\widehat{NAM}\)

=> Tam giác NMA đồng dạng tam giác NFM (gg)
=> \(\frac{NM}{NF}=\frac{NA}{NM}\)\(\Rightarrow NM^2=AN\cdot NF\left(1\right)\)

Ta có: \(\widehat{MFB}=\widehat{MHB}=90^o\)=> Tứ giác MFHB nội tiếp

\(\Rightarrow\widehat{FHN}=\widehat{FBM}\)mà \(\widehat{FBM}=\widehat{NAH}\)

\(\Rightarrow\widehat{NAH}=\widehat{FHN}\)

\(\Rightarrow\Delta NAH\)đồng dạng \(\Delta NHF\left(g.g\right)\)

\(\Rightarrow\frac{NA}{NH}=\frac{NH}{NF}\Rightarrow NH^2=NA\cdot NF\left(2\right)\)

(1)(2) => NM²=NH² => MN=NH (đpcm)

a: ΔODE cân tại O

mà OM là trung tuyến

nên OM vuông góc DE

=>góc OMA=90 độ=góc OCA=góc OBA

=>O,A,B,M,C cùng thuộc 1 đường tròn

b: Xét ΔBSC và ΔCSD có

góc SBC=góc SCD

góc S chung

=>ΔBSC đồng dạng với ΔCSD

=>SB/CS=SC/SD

=>CS^2=SB*SD

góc DAS=gócEBD

=>góc DAS=góc ABD

=>ΔSAD đồng dạng với ΔSBA

=>SA/SB=SD/SA

=>SA^2=SB*SD=SC^2

=>SA=SC
c; BE//AC

=>EH/SA=BH/SC=HJ/JS

mà SA=SC
nênHB=EH

=>H,O,C thẳng hàng