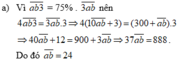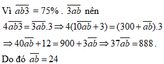a3b= ab.11= a(a+b)b

=>a+b=3

=>ab=12; ab=-12 hoặc ab=21; ab=-21

Vậy ab thuộc {12;-12;21;-21}

\(a\cdot10\cdot11+b\cdot11=1\cdot100+3\cdot10+b\)

\(a\cdot10+b\cdot10=3\cdot10\)

\(a+b=3=1+2=2+1\)

\(\Rightarrow\hept{\begin{cases}a=1\\b=2\end{cases}}\hept{\begin{cases}a=2\\b=1\end{cases}}\)

Ta có: ab. 11 =  a3b

        \(\Rightarrow\left(a.10+b\right).11=a.100+30+b\)

         \(\Rightarrow a.110+b.11=a.100+b+30\)

          \(\Rightarrow10a+10b=30\)    ( bớt 2 vế  cho 100a+b )

          \(\Rightarrow10\left(a+b\right)=30\)

          \(\Rightarrow a+b=30:10=3\) 

          \(\Rightarrow a+b=1+2=0+3\)

   Mà a là chữ số hàng chục nên khác 0 suy ra \(ab\in\left\{30;21;12\right\}\)

ab3 = ab + 288

ab . 10 + 3 = ab + 288

ab.10 - ab + 3 = 288 

ab . 9 + 3 = 288 

ab . 9 = 288 - 3

ab . 9 = 285

ab = 285 : 9

ab = ?

Vì ab3 = \(\frac{3}{4}\). 3ab

\(\Rightarrow\)ab3 = 3ab . \(\frac{3}{4}\)

\(\Rightarrow\)10ab + 3 = ( 300 + ab ) . \(\frac{3}{4}\)

\(\Rightarrow\)10ab + 3 = 225 + \(\frac{3}{4}\). ab

\(\Rightarrow\)10ab - \(\frac{3}{4}\). ab = 225 - 3

\(\Rightarrow\)\(\frac{37}{4}\). ab = 222

\(\Rightarrow\)ab = 222 : \(\frac{37}{4}\)= 24

Vậy số tự nhiên có 2 chữ số cần tìm là 24

24 mình cũng có ý kiến như bạn SKT _NTT

Mình cũng nghĩ là 24.

story to bam nham

tạp nham à

black boy và bboy công nghệ là 1 à để hình giống nhau z

\(a^4+b^4-a^3b-ab^3=a^3\left(a-b\right)-b^3\left(a-b\right)=\left(a-b\right)\left(a^3-b^3\right)=\left(a-b\right)\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^2\left(a^2+ab+b^2\right)\)

Có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\a^2+ab+b^2>0\end{matrix}\right.\)

\(\Rightarrow a^4+b^4-a^3b-ab^3\ge0\)

\(\Rightarrow a^4+b^4\ge a^3b+ab^3\)

Áp dụng BĐT cosi với 2 số không âm:

`a^4+b^4+b^4+b^4>=4\root4{a^4b^12}=4|ab^3|>=4ab^3`

Hoàn toàn tương tự:

`b^4+a^4+a^4+a^4>=4a^3b`

`=>a^4+b^4+b^4+b^4+b^4+a^4+a^4+a^4>=4ab^3+4a^3b`

`<=>4(a^4+b^4)>=4(ab^3+a^3b)`

`<=>a^4+b^4>=ab^3+a^3b`