abcd = 2401 

3456 nha bạn

Đáp án cần chọn là: A

trình bày ra nhé :)

ai hiểu

gấp k

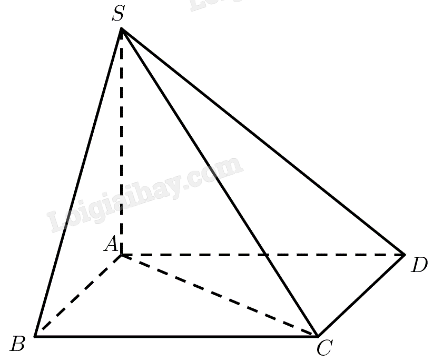
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)

Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)

\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)

Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).

b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)

Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)

\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)

Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).

c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)

\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)

Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).

Ta có:

abcd chia hết cho 3 và 5 nên d phải là tận cùng bằng 5 hoặc 0

⇒a+b+c+d  phải chia hết cho 3

từ đó ta rút ra có 2 số chia hết cho 5 là 8765 và 3210 nhưng vì 8765 không chia hết cho 3 

⇒ số đó là 3210

Có  4 cách chia:

Cách chia bi nhiều túi nhất là cách 4,ta được 6 túi ,

Lần lượt chia đều bi đỏ vào 6 túi;

48:6= 8 (viên mỗi túi) 

Chia đều bi xanh vào 6 túi;

30 :6=5 (viên mỗi túi)

Chia đều bi vàng vào 6 túi;

66:6=11 (viên mỗi túi)

Tổng cộng số viên bi trong mỗi túi ;

8+5+11=24 (viên mỗi túi)