Công thức nghiệm pt bậc 2 và hằng đẳng thức

Những câu hỏi liên quan
2:Khi nào hệ pt có nghiệm duy nhất?Vô nghiệm?Vô số nghiệm?(mỗi trường hợp cho 1 VD)3:Lấy 3 vd về hàm số bậc nhất?Lấy 3 vd về hàm số bậc 2?4:Viết công thức nghiệm giải pt bậc 25:Nếu các bước giải bài toán cách lập pt hoặc hệ pt6:Phát biểu định lý Vi-ét và cách nhẩm nghiệm7:Nêu định nghĩa,tính chất,dấu hiệu nhận biết về tứ giác nội tiếp8:Nêu cách chứng minh đẳng thức tích9:Nêu cách chứng minh tứ giác nội tiếp
Đọc tiếp
2:Khi nào hệ pt có nghiệm duy nhất?Vô nghiệm?Vô số nghiệm?
(mỗi trường hợp cho 1 VD)
3:Lấy 3 vd về hàm số bậc nhất?Lấy 3 vd về hàm số bậc 2?
4:Viết công thức nghiệm giải pt bậc 2
5:Nếu các bước giải bài toán = cách lập pt hoặc hệ pt
6:Phát biểu định lý Vi-ét và cách nhẩm nghiệm
7:Nêu định nghĩa,tính chất,dấu hiệu nhận biết về tứ giác nội tiếp
8:Nêu cách chứng minh đẳng thức tích
9:Nêu cách chứng minh tứ giác nội tiếp
9:Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Chứng minh tứ giác có tổng 2 góc đối bằng 180°
Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau. Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.
Đúng 1
Bình luận (2)
7:dấu hiệu :Tứ giác có tổng hai góc đối bằng 180∘ . - Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó. - Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
định nghĩa: Trong Hình học phẳng, một tứ giác nội tiếp là một tứ giác mà cả bốn đỉnh đều nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên. Tâm và bán kính đường tròn lần lượt được gọi là tâm đường tròn ngoại tiếp và bán kính đường tròn ngoại tiếp.
tính chất: Trong tứ giác nội tiếp, cặp hai tam giác đối nhau qua giao hai đường chéo đồng dạng với nhau. trong đó E và F lần lượt là giao điểm hai cặp cạnh đối của tứ giác. Với một bộ bốn cạnh là bốn cạnh một tứ giác nội tiếp, có thể thay đổi thứ tự các cạnh theo một trật tự bất kỳ
Đúng 1
Bình luận (0)
6: viet thuận:
Cho phương trình bậc 2 một ẩn: ax2+bx+c=0 (a≠0) (*) có 2 nghiệm x1 và x2. Khi đó 2 nghiệm này thỏa mãn hệ thức sau:
Hệ quả: Dựa vào hệ thức Viet khi phương trình bậc 2 một ẩn có nghiệm, ta có thể nhẩm trực tiếp nghiệm của phương trình trong một số trường hợp đặc biệt:
Nếu a+b+c=0 thì (*) có 1 nghiệm x1=1 và x2=c/aNếu a-b+c=0 thì (*) có nghiệm x1=-1 và x2=-c/aviet đảoGiả sử hai số thực x1 và x2 thỏa mãn hệ thức:
phép nhẩm: “Phân tích hệ số ![]() thành tích và
thành tích và ![]() thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số
thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số ![]() trước rồi kết hợp với
trước rồi kết hợp với ![]() để tìm ra hai số thỏa mãn tích bằng
để tìm ra hai số thỏa mãn tích bằng ![]() và tổng bằng
và tổng bằng ![]() .
.
Đúng 1
Bình luận (9)
Xem thêm câu trả lời
hằng đẳng thức bậc cao ?
(6) (a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)(a+b+c)3=a3+b3+c3+3(a+b)(b+c)(c+a)
(7) a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ac)
(8) (a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)(a−b)3+(b−c)3+(c−a)3=3(a−b)(b−c)(c−a)
(9) (a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2(a+b)(b+c)(c+a)−8abc=a(b−c)2+b(c−a)2+c(a−b)2
(10) (a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)−abc
(11) ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33ab2+bc2+ca2−a2b−b2c−c2a=(a−b)3+(b−c)3+(c−a)33
(12)ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3ab3+bc3+ca3−a3b−b3c−c3a=(a+b+c)[(a−b)3+(b−c)3+(c−a)3]3
(13) an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)an−bn=(a−b)(an−1+an−2b+an−3b2+...+a2bn−3+abn−2+bn−1)
(14) Với n lẻ:
an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)an+bn=(a+b)(an−1−an−2b+an−3b2−...+a2bn−3−abn−2+bn−1)
(15) Nhị thức Newton:
(a+b)n=an+n!(n−1)!1!an−1b+n!(n−2)!2!an−2b2+...+n!(n−k)!k!an−kbk+...+n!2!(n−2)!a2bn−2+n)!1!(n−1)!abn−1+bn
Đúng 0
Bình luận (0)
Nêu định nghĩa căn bậc hai số học? Các quy tắc,hằng đẳng thức về căn thức
Căn bậc hai số học của một số nguyên dương x là a sao cho
\(\left\{{}\begin{matrix}a>0\\a^2=x\end{matrix}\right.\)
Hằng đẳng thức về căn thức là:
\(\sqrt{A^2}=\left|A\right|\)
Quy tắc:
\(\sqrt{A^2\cdot B}=\sqrt{B}\cdot\left|A\right|\)
\(\sqrt{\dfrac{A}{B}}=\dfrac{\sqrt{A}}{\sqrt{B}}\)
\(\sqrt{A\cdot B}=\sqrt{A}\cdot\sqrt{B}\)
Đúng 1
Bình luận (0)
số hữu tỉ la j căn bậc 2 hằng đẳng thức
Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
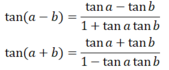
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
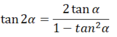
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
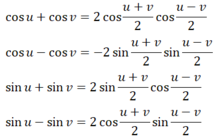
Đúng 0
Bình luận (0)
điền số thích hợp vào các đẳng thức sau
căn bậc 2 của 1 =.........
căn bậc 2 của 1+2+1=.............
căn bậc 2 của 1+2+3+2+1=..........
hãy viết tiếp 3 đẳng thức nửa vào đẳng thức trên
hãy viết công thức tổng quát
Chứng tỏ rằng đa thức x^2+2x+2 không có nghiệm...đừng giải theo kiểu hằng đẳng thức
dể đa thức x^2 +2x +2 có nghiệm nên suy ra x thuộc ước của 2
thay x lần lượt suy ra pt vô nghiệm
Đúng 0
Bình luận (0)
Bài này bn phải phân tích ra đưa về dạng 1 hằng đẳng thức(=(x+1)2) rồi suy ra vô nghiệm, ko nên giải theo cách khác
Đúng 0
Bình luận (0)
tại sao x lại thuộc Ư(2) ???
MÀ chưa học hằng đẳng thức nữa
Đúng 0
Bình luận (0)
khai triển hằng đẳng thức
(x+1)^2-y^2(có công thức nha)
= (x+1-y)(x+1+y)
hằng đẳng thức số 3: a^2 - b^2 = (a-b)(a+b)
\(\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
( x + 1 )2 - y2
= ( x - y + 1 )( x + y + 1 )
Xem thêm câu trả lời
mn ơi cho e xin công thức của hằng đẳng thức số 6 và 7 nha
công thức :
6.tổng hai lập phương :
A3 + B3 = ( A+B).(A2 - AB + B2 )
7. hiệu hai lập phương :
A3 - B3 = ( A-B).( A2+ AB + B2 )
*Sxl
công thức 6.Tổng 2 lập phương
với a và b là biểu thức tùy ý ta có:A3+B3 =(A+B)(A2-AB+B2)
công thức 7:hiệu 2 lập phuong
A3-B3=(A-B)(A2+AB+B2)
khó quá và dài lắm cơ
nhớ k cho ...nha
học tốt
Xem thêm câu trả lời
























