Giúp mk với câu 25 giải PT ạ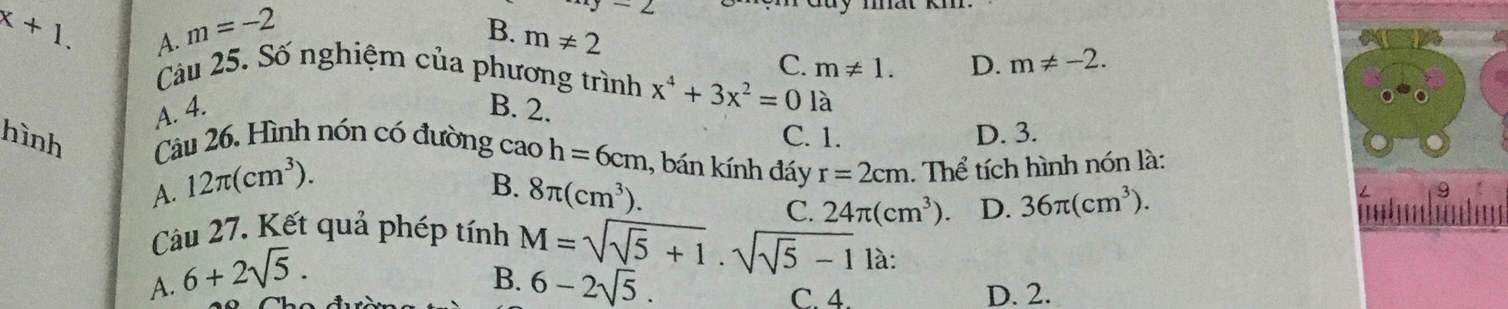

Những câu hỏi liên quan
giải pt tích sau : 1/9(x-3)^2 -1/25 (x+5)^2=0
giải chi tiết giúp mk với ạ
`1/9(x-3)^2-1/25(x+5)^2=0`
`<=>(1/3x-1)^2-(1/5x+1)^2=0`
`<=>(1/3x-1-1/5x-1)(1/3x-1+1/5x+1)=0`
`<=>(2/15x-2). 8/15x=0`
`<=>2/15x-2=0` hoặc `8/15x=0`
`<=>x=15` hoặc `x=0`
Vậy `S=`{`15;0`}
Đúng 2
Bình luận (0)
Giải pt: (X^2-2x-3).(X^2+10x+21)=25
^ : mũ
Giúp mk vs ạ
(x2 - 2x - 3)(x2 + 10x + 21) = 24
<=> (x - 3)(x + 1)(x + 3)(x + 7) = 24
<=> (x2 + 4x - 21)(x2 + 4x + 3) = 24
Đặt x2 + 4x - 21 = a
=> PT <=> a(a + 24) = 24
<=> a2 + 24a - 24 = 0
Tới đây thì đơn giản rồi nên b làm tiếp nhé
Đúng 0
Bình luận (0)
ủa mà bạn KQ sau dấu = là 25 mà sao bạn lai làm là 24 ???????????
Đúng 0
Bình luận (0)
Lỡ rồi. B sửa thành 25 đi. Không có khác gì mấy đâu
Đúng 0
Bình luận (0)
cho hệ pt \(\hept{\begin{cases}mx+my=-3\\\left(1-m\right)x+y=0\end{cases}}\)
a, giải hệ với m=2
b, tìm m để hệ có nghiệm âm
Giúp mk vs ạ câu a mk lm đk oy còn câu b ạ!!
Thanks m.n nhìu ạ!!!!!
\(\hept{\begin{cases}mx+my=-3\\\left(1-m\right)x+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}mx+m.\left(m-1\right)x=-3\\y=\left(m-1\right)x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m^2x=-3\\y=\left(m-1\right)x\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{-3}{m^2}\\y=\left(m-1\right).\frac{-3}{m^2}\end{cases}}\)
Để phương trình có nghiệm âm thì ta có
\(\hept{\begin{cases}\frac{-3}{m^2}< 0\\\frac{-3.\left(m-1\right)}{m^2}< 0\end{cases}}\Leftrightarrow m>1\)
Đúng 0
Bình luận (0)
GIÚP EM BÀI GIẢI PT VÀ CÂU C,D,E BÀI 2 VỚI Ạ..
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
Đúng 2
Bình luận (0)
Giải pt
(x^2+x-2)^2=3(x^4+x^2+1)
giải giúp mk với ạ
\(\left(x^2+x-2\right)^2=3\left(x^4+x^2+1\right)\)
\(\Leftrightarrow\left[\left(x-1\right)\left(x+2\right)\right]^2=3\left(x^4+x^2+1\right)\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)^2=3\left(x^4+x^2+1\right)\)
\(\Leftrightarrow x^4+4x^3+4x^2-2x^3-8x^2-8x+x^2+4x+4=3x^4+3x^2+3\)
\(\Leftrightarrow x^4+2x^3-3x^2-4x+4-3x^4-3x^2-3=0\)
\(\Leftrightarrow-2x^4+2x^3-6x^2-4x+1=0\)
Đúng 0
Bình luận (0)
giúp mk bài này vs ạ (giải theo pp lập hệ pt) của lớp 9
MK CẦN LỜI GIẢI CHI TIẾT Ạ
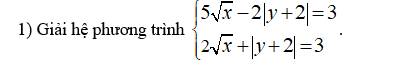

câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)
Đúng 0
Bình luận (2)
Câu 2:
Gọi thời gian đội A hoàn thành công việc khi làm một mình là x(x>15)
=>thời gian đội B hoàn thành công việc khi làm một mình là x-15
Theo đề, tacó: \(\dfrac{1}{x}+\dfrac{1}{x-15}=\dfrac{1}{10}\)
=>\(\dfrac{x-15+x}{x\left(x-15\right)}=\dfrac{1}{10}\)
=>x^2-15x=10(2x-15)
=>x^2-15x-20x+150=0
=>x^2-35x+150=0
=>(x-30)(x-5)=0
=>x=30(nhận) hoặc x=5(loại)
=>Đội B cần 15 ngày
Đúng 1
Bình luận (1)
Cho pt 5x²–12x–m–3=0
a) giai pt khi m=2
b) tìm m để pt 2 nghiệm x1,x2 thoã mãn 2x1–x2= 1
Câu a mk giai đc rồi,mong giúp câu b khoa quá làm ơn giải chi tiết ra hết luôn nhé..cảm ơn ạ
Câu 23, 24 và 25 ạ
Giải chi tiết ra giúp em với ạ

23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
Đúng 1
Bình luận (0)
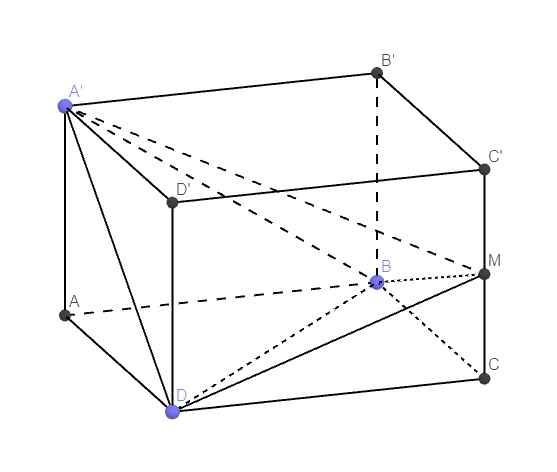
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
giải pt: \(\dfrac{x+1}{3}=x+3\)
giúp mk vs ạ mk cần gấp
\(\Leftrightarrow x+1=3x+9\\ \Leftrightarrow2x=-8\\ \Leftrightarrow x=-4\)
Đúng 1
Bình luận (0)