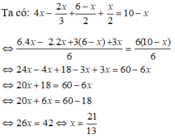\(\frac{21}{x^2-4x+10}-x^2+4x-6\ge0\Leftrightarrow\frac{21}{x^2-4x+10}-\left(x^2-4x+10\right)+4\ge0\)

Đặt \(t=x^2-4x+10=\left(x-2\right)^2+6\), ta có điều kiện \(t\ge6\), khi đó \(t>0\)

Phương trình ban đầu tương đương : \(\frac{21}{t}-t+4\ge0\Leftrightarrow t^2-4t-21\le0\)

                                                                               \(\Leftrightarrow-3\le t\le7\)

Kết hợp với điều kiện \(t\ge6\), ta được \(6\le t\le7\)

Do đó :

\(\frac{21}{x^2-4x+10}-x^2+4x-6\ge0\Leftrightarrow\begin{cases}\left(x-2\right)^2+6\ge6\\\left(x-2\right)^2+6\le7\end{cases}\)

                                           \(\Leftrightarrow\left|x-2\right|\le1\)

                                          \(\Leftrightarrow1\le x\le3\)

Vậy tập nghiệm của bất phương trình đã cho là \(T=\left[1;3\right]\)

mk tên phạm thảo vân đó

\(\Leftrightarrow\left(x^2-4x+6\right)\cdot\left(x^2-4x+10\right)=21\)

\(\Leftrightarrow\left(x^2-4x+6\right)\cdot\left(x^2-4x+10\right)-21=0\)

\(\Leftrightarrow x^4-4x^3+10x^2-4x^3+16x^2-40x+6x^2-24x+60-21=0\)

\(\Leftrightarrow x^4-8x^3+32x^2-64x+39=0\)

\(\Leftrightarrow x^4-x^3-7x^3+7x^2+25x^2-25x-39x+39=0\)

\(\Leftrightarrow x^3\left(x-1\right)-7x^2\cdot\left(x-1\right)+25x\left(x-1\right)-39x\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\cdot\left(x^3-7x^2+25x-39\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^3-3x^2-4x^2+12x+13x-39\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[x^2\left(x-3\right)-4x\cdot\left(x-3\right)+13\left(x-3\right)\right]=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-4x+13\right)=0\)

\(\hept{\begin{cases}x-1=0\\x-3=0\\x^2-4x+13=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\x=3\\x\notin R\end{cases}}\)

Vậy phương trình của tập nghiệm là S={1;3}

a, Đặt \(x^2-4x+8=a\left(a>0\right)\)

\(\Rightarrow a-2=\frac{21}{a+2}\)

\(\Leftrightarrow a^2-4=21\Rightarrow a^2=25\Rightarrow a=5\)

Thay vào là ra

b) ĐK: \(y\ne1\)

bpt <=> \(\frac{4\left(1-y\right)}{1-y^3}+\frac{1+y+y^2}{1-y^3}+\frac{2y^2-5}{1-y^3}\le0\)

<=> \(\frac{3y^2-3y}{1-y^3}\le0\)

\(\Leftrightarrow\frac{y\left(y-1\right)}{\left(y-1\right)\left(y^2+y+1\right)}\ge0\)

\(\Leftrightarrow\frac{y}{y^2+y+1}\ge0\)

vì \(y^2+y+1=\left(y+\frac{1}{2}\right)^2+\frac{3}{4}>0\)

nên bpt <=> \(y\ge0\)

Chọn đáp án A

Lời giải:
ĐKXĐ: $x\geq \frac{-3}{2}$

PT $\Leftrightarrow x^2-4x+21-6\sqrt{2x+3}=0$

$\Leftrightarrow (x^2-6x+9)+[(2x+3)-6\sqrt{2x+3}+9]=0$

$\Leftrightarrow (x-3)^2+(\sqrt{2x+3}-3)^2=0$

Ta thấy: $(x-3)^2\geq 0; (\sqrt{2x+3}-3)^2\geq 0$ với mọi $x\geq \frac{-3}{2}$

Do đó để tổng của chúng bằng $0$ thì:
$(x-3)^2=(\sqrt{2x+3}-3)^2=0$

$\Leftrightarrow x=3$ (tm)