Cho tam giác ABC có B= 60 độ,phân giác B cắt AC tại D.Từ A kẻ đường thẳng song song với BC cắt tia BD tại E
a)Chứng minh tam giác ABE cân
b)Tính góc BAE
cho tam giác ABC có góc B bằng 60 độ vẽ phân giác Bd từ A kẻ đường thẳng vuông góc với BD cắt BD tại H và cắt BC tại E.
a) tính số đo góc BAH chứng minh tam giác ABE là tam giác cân
b) chứng minh tam giác DBA và am giác DBE
c) từ E jer đường thẳng song song với BD cắt đường thẳng BC tại F . Chứng minh tam giác ABF cân
Câu 5: Cho ABC vuông tại A (AB < AC).Tia phân giác góc ABC cắt AC tại D;vẽ DE
vuông góc BC tại E
a/ Chứng minh tam giác SAD = tam giác BED
b/ AE cắt BD tại H.Chứng minh tam giác BAE cân và H là trung điểm AE
c/ Qua E vẽ đường thẳng song song BD cắt AC tại F;FH cắt DE tại G.Chứng minhDE = 3GD
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>BA=BE và DA=DE
=>ΔBAE cân tại B và BD là trung trực của AE
=>H là trung điểm của AE
Cho tam giác ABC. Vẽ tia phân giác BD của góc B. Từ A kẻ đường thẳng song song với BD cắt tia đối của BC tại E. Tia phân giác của các góc ABE cắt AE tại D
a. Nếu góc ABC=60 độ thì góc EAB=?
b. Chứng tỏ BAE=BEA
Mọi người giúp mình nhé mai mình phải nộp r
Bài 1/ cho tam giác ABC có góc BAC =100 độ;góc ACB=30.Tia phân giác của góc ABC cắt AC tại D.Qua A kẻ đường thẳng song song với BD;đường thẳng này cắt BC tại E .Kẻ BH vuông góc AE tại H.
a/ tính góc ABE,AEB,EAB
b/ CM tam giác ABH=EBH
c/ Qua A kẻ đường thẳng song song với BC ,đường thẳng này cắt BD tại F .CM AB=À
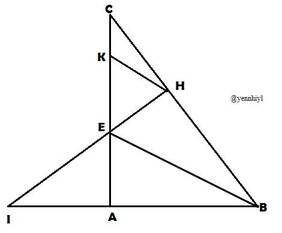
Cho tam giác ABC vuông ở A có góc B bằng 60 độ . Tia phân giác của góc ABC cắt AC ở E. Kẻ EH vuông góc với BC
a) Chứng minh tam giác ABE bằng tam giác HBE
b) Chứng minh HB = HC
c) Từ H kẻ đường thẳng song song với BE cắt AC ở K. Chứng minh tam giác EHK đều
d) Gọi I là giao điểm của BA và HE. Chứng minh IE > EH
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
Bài 1. Cho tam giác ABC có A= 80◦ và 2B = 3C. a) Tính các góc B và C. b) Tia phân giác của góc B cắt AC tại D. Đường thẳng qua A song song với BD cắt tia CB tại E. Chứng minh rằng tam giác ABE cân. c) Tia phân giác của góc ABE cắt AE tại F. Chứng minh rằng BF là đường trung trực của AE.
a: \(\widehat{B}=60^0;\widehat{C}=40^0\)
. Cho tam giác ABC có AB < AC. Gọi Ax là tia phân giác của góc A. Qua trung điểm M của BC kẻ đường thẳng vuông góc với Ax, cắt các đường thẳng AB, AC lần lượt tại D và E.
a) Chứng minh tam giác DAE cân
b) Qua B kẻ đường thẳng song song với AC, cắt DE tại F. Chứng minh tam giác BDF cân tại B.
c) Chứng minh BD = CE.
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>MF=ME
=>M là trung điểm của EF
=>BD=CE
tam giác ABC có tia phân giác của góc B cắt AC ở D.Qua A kẻ đường thẳng song song với BD cắt BC tại E.CMR:góc BAE=góc BEA
Cho tam giác ABC có tia phân giác góc B cắt AC ở D. Qua A kẻ đường thẳng song song với BD, đường thẳng này cắt đường thẳng BC ở E. Chứng minh rằng góc BAE=góc BEA
đổi hình rùi nè đẹp hơn trước kho mấy anh