Điểm A nằm ngoài đường tròn (O) kẻ tiếp tuyến ABC vầ AMN, BN cắt CM tại S
Cmr
a, \(\widehat{A}+\widehat{BSM}=2\widehat{CBN}\)
b, AM. AN= AB.AC
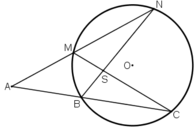
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn. Chứng minh \(\widehat{A}+\widehat{BSM}=2.\widehat{CMN}.\)
cho điểm A bên ngoài đường tròn (O) vẽ 2 cát tuyến ABC và AMN sao cho 2 đường thẳng BN và CM cắt nhau tại điểm S nằm bên trong đường tròn.
Chứng minh :
\(\widehat{A}\)+\(\widehat{BSM}\)= \(2.\widehat{CMN}\)
Qua điểm $A$ nằm ngoài đường tròn tâm $O$, kẻ các cát tuyến $ABC$ và $ADE$ sao cho $BE$ và $CD$ cắt nhau tại $M$. Chứng minh $\widehat{A}+\widehat{CME}=2 \widehat{CDE}$.
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh A ^ + B S M ⏞ = 2 ⋅ C M N ⏞

Kiến thức áp dụng
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh A ^ + B S M ^ = 2 . C M N ^
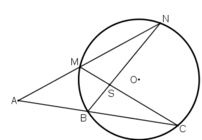

⇒ A ^ + B S M ^
= 1 2 . s đ N C ⏜ - s đ B M ⏜ + 1 2 s đ N C ⏜ + s đ M B ⏜ = s đ N C ⏜ 1
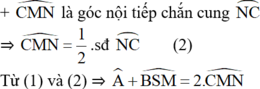
(đpcm)
Cho một điểm A ở ngoài đường tròn (O). Kẻ hai cát tuyến AMN và APQ tới đường tròn sao cho MN > PQ. Dựng đường tròn (O ; OA). Kẻ hai dây AD và AF của đường tròn lớn tiếp xúc với đường tròn nhỏ tại B và C. Cát tuyến AMN và cát tuyến APQ cắt đường tròn lớn ở E và H.
a) Chứng minh AD = AF;
b) Chứng minh AE > AH;
c) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn;
d) So sánh $\widehat{OAE}$ và $\widehat{OAH}$.
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI MN, OK PQ.
Trong đường tròn nhỏ, ta có: MN > PQ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d)
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI MN, OK PQ.
Trong đường tròn nhỏ, ta có: MN > PQ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d)
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI MN, OK PQ.
Trong đường tròn nhỏ, ta có: MN > PQ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d)
(TP HCM - 2020)
Cho đường tròn tâm $O$, bán kính $R$ và điểm $A$ nằm ngoài đường tròn sao cho $OA > 2R$. Từ $A$ kẻ 2 tiếp tuyến $AD;$ $AE$ đến đường tròn $(O)$ ($D$, $E$ là 2 tiếp điểm). Lấy điểm $M$ nằm trên cung nhỏ $\overset{\frown}{DE}$ sao cho $MD > ME$. Tiếp tuyến của đường tròn $(O)$ tại $M$ cắt $AD$; $AE$ lần lượt tại $I$; $J$. Đường thẳng $DE$ cắt $OJ$ tại $F$.
a. Chứng minh: $OJ$ là đường trung trực của đoạn thẳng $ME$ và $\widehat{OMF} = \widehat{OEF}$.
b. Chứng minh: tứ giác $ODIM$ nội tiếp và 5 điểm $I$; $D$; $O$; $F$; $M$ cùng nằm trên một đường tròn.
c. Chứng minh $\widehat{JOM} = \widehat{IOA}$ và $\sin \widehat{IOA} = \dfrac{MF}{IO}$.
Cho đường tròn (O) đường kính NP và điểm M nằm ngoài đường tròn . Từ điểm M kẻ tiếp tuyến MN ( N là tiếp điểm ) , cắt tuyến MDP ( D nằm giữa M và P ) . Qua P kẻ PE // OM ( E thuộc đường tròn (O)) . Kẻ NE cắt OM tại H
a) MN2 = MD . MP
b) HN = HE
c) \(\widehat{OPH}=\widehat{OMP}\)
a) MN là tiếp tuyến đường tròn (O) \(\Rightarrow\widehat{MNP}=90^o\)
DO = ON = OP => \(DO=\frac{1}{2}NP\Rightarrow\widehat{NDP}=90^o\)
- Aps dụng hệ thức lượng cho tam giác MNP vuông tại N đường cao ND , ta có :
MN2 = MD . MP ( đpcm )
b) Ta có : PE // OM => PE // OH
Mà O là trung điểm của NP => OH là đường trung bình của tam giác ENP
=> H là trung điểm NE
Vậy : HN = HE ( đpcm )
c) Theo ( c/m câu b ) : HN = HE => \(HE\perp OM\)
Áp dung hệ thức trong tam giác NMO vuông tại N , đường cao NH :
Ta có : ON2 = OM . OH => OP2 = OM . OH
\(\Rightarrow\frac{OP}{OM}=\frac{OH}{OP}\left(1\right)\)
- Xét 2 tam giác: OHP và OPM
có : \(\frac{OP}{OM}=\frac{OH}{OP}\left(theo\left(1\right)\right)\)
\(\widehat{O}\)là góc chung
Do đó : \(\Delta OHP~\Delta OPM\left(c-g-c\right)\)
\(\Rightarrow\widehat{OPH}=\widehat{OMP}\left(đpcm\right)\)
Mọi người giúp em ý 4 với ạ
Cho (O; R). Từ điểm A ở ngoài đường tròn vẽ 2 tiếp tuyến AM, AN (M, N là 2 tiếp điểm). Qua A kẻ cát tuyến AEF với đường tròn (O) (E nằm giữa A và F). Qua O kẻ đường thẳng OD vuông góc với EF (D thuộc EF. Đường thẳng OD cắt AM, AN lần lượt tại B và C.
1) Chứng minh bốn điểm A, D, O, N thuộc một đường tròn
2) Chứng minh: AM2 = AE.AF. Biết AM = 6cm; AF = 9cm. Tính độ dài đoạn thẳng EF.
3) Chứng minh rằng: \(\widehat{MDB}\)= \(\widehat{NDC}\)
4) Đường thẳng qua O vuông góc với BC cắt MN tại I, AI cắt CB tại H. Chứng minh H là trung điểm của CB.