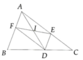
Cho ABC, đường thẳng d cắt cạnh AB, AC ở E,F; cắt cạnh BC kéo dài ở I
CMR: AE/EB x BI/IC x CF/FA =1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho tam giác ABC (AB = AC). Tia phân giác Ax của góc A cắt BC ở D. Từ D kẻ đường thẳng song song với AB cắt AC ở F. Từ D kẻ đường thẳng song song với AC cắt AB ở E. a) Chứng minh AE = ED = DF =
FA.
b) Từ trung điểm M của cạnh BC kẻ đường thẳng vuông góc với tia Ax cắt các đương thắng AB và AC ở P và Q. Chứng minh EF song song với PQ.
c) Chứng minh BP =CQ.
1. Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song AB và AC chúng cắt AB,AC theo thứ tự ở E và F. Chứng minh hệ thức: AE/AB+AF/AC=1
2. Cho tam giác ABC, 1 đường thẳng song song với BC cắt các cạnh AB, AC theo thứ tự ở D và E. Qua C kẻ đường thẳng song song với EB cắt AB ở F. Chứng minh hệ thức AB2=AD*AF
3.Cho tam giác ABC( AB<AC) đường phân giác AD. Qua trung điểm M của BC kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. Chứng minh rằng:
a. AE=AK
b. DK=CE
cho tam giác abc nhọn trên cạnh ab lấy d qua d kẻ đường thẳng // bc cắt ac ở e qua c kẻ đường thẳng //ab cắt de tại f bf cắt ac tại h
a) tam giác abc đồng dạng tam giác cfe
b)c/m he/hc=ef=df
c)qua e kẻ đường thẳng // ab cắt af tại i
cm 1/ie=1/ad=1/cf
a: Xét ΔABC và ΔCFE có
góc ACB=góc CEF=góc AED
góc BAC=góc FCE
=>ΔABC đồng dạng vơi ΔCFE
b: Xét ΔHEF và ΔHCB có
góc HEF=góc HCB
góc FHE=góc BHC
=>ΔHEF đồng dạng vơi ΔHCB
=>HE/HC=EF/BC=EF/DF
. Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua C vuông góc với BD cắt Ab ở F. Chứng minh rằng D, E, F thẳng hàng
Cho tam giác ABC , D là 1 điểm trên cạnh BC , Qua C kẻ đưởng thẳng song song với AC cắt AB ở E . Qua D kẻ đường thẳng song song với AB cắt AC ở F có EF // BC . Chứng minh D là trung điểm cạnh BC
Cho tam giác ABC, D là trung điểm của cạnh AB. Đường thẳng qua B song sog vs cạnh BC cắt AC ở E, đường thẳng qua E sog sog với cạnh AB cắt BC ở F. cmr:
a)AD=EF
b)AE=EC, BF=FC.
a: Xét tứ giác ADFE có
AD//FE
AE//DF
Do đó: ADFE là hình bình hành
Suy ra: AD=EF
b: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
hay AE=EC
Xét ΔABC có
E là trung điểm của AC
EF//AB
Do đó: F là trung điểm của BC
hay BF=FC
Cho tam giác ABC. Dựng đường thẳng song song với BC, cắt cạnh AB ở E, cắt cạnh AC ở F sao cho BE = AF
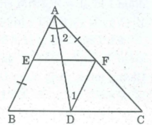
Cách dựng:
- Dựng đường phân giác AD của góc BAC.
- Qua D dựng đường thẳng song song AB cắt AC tại F.
- Qua F dựng đường thẳng song song với BC cắt AB tại E.
Ta có điểm E, F cần dựng.
Chứng minh:
DF // AB
⇒ ∠ A 1 = ∠ D 1 (so le trong)
Lại có: ∠ A 1 = ∠ A 2 ( vì AD là tia phân giác của góc BAC).
Suy ra: ∠ D 1 = ∠ A 2
⇒ ∆ AFD cân tại F ⇒ AF = DF (l)
DF // AB hay DF // BE
EF // BC hay EF // BD
Tứ giác BDFE là hình bình hành ⇒ BE = DF (2)
Từ (1) và (2) suy ra: AF = BE.
Cho tam giác ABC (AB<AC). Đường phân giác AD của góc A cắt cạnh BC ở D, từ trung điểm M của BC kẻ đường thẳng // với AD cắt AC tại F và cắt đường thẳng AB tại E. Chứng minh BE = CF.
Cho tam giác ABC (AB<AC). Đường phân giác AD của góc A cắt cạnh BC ở D, từ trung điểm M của BC kẻ đường thẳng // với AD cắt AC tại F và cắt đường thẳng AB tại E. Chứng minh BE = CF.
Cho tam giác ABC điểm D thuộc cạnh BC. Từ D kẻ đường thẳng song song với cạnh AB, cắt cạnh AC tại E và đường thẳng qua D song song với AC cắt AB tai F. Chứng minh hai điểm E và F đối xứng với nhau qua trung điểm I của đoạn thẳng AD
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I