Cho hình thang cân ABCD có đáy CD=14cm;cạnh bên AD=căn 32 cmvà góc ADC= 45 độ. Diện tích hình thang cân ABCD là .....cm

Những câu hỏi liên quan
Cho hình thang cân ABCD có đáy CD=14cm,cạnh bên \(AD=\sqrt{32}\)cm và và góc ADC =45 độ.Tính diện tích hình thang cân ABCD ?
1, Cho hình thang cân ABCD có đáy nhỏ AB, đường cao AH=2cm. Biết HC=3,5cm và HD=1,5cm. Tính chu vi của hình thang này 2, Cho hình thang cân ABCD có cạnh bên AD=5cm, các cạnh đáy AB=6cm và CD=14cm. Tính chiều cao của hình thang. XIN HÃY GIÚP MÌNH Ạ, xin cảm ơn 🌹❤️
Bài 1. Cho hình thang cân ABCD (AB\\CD) có AB=8cm, BC=AD=5cm, CD=14cm. Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Chứng minh: CD-AB=2AK. Từ đó tính độ dài BH.
c) Tính diện tích hình thang ABCD.
Bài 2. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc BCD.
Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Đúng 2
Bình luận (0)
Cho hình thang cân ABCD có đáy CD=14cm ;cạnh bên AD=\(\sqrt{32}\) và góc ADC=.45
Diện tích hình thang cân ABCD là
hình tự vẽ nha bạn
kẻ đường cao AH=> tam giác AHD vuông cân tại H
=> AH=DH
áp dụng Pitago => AH=DH=4cm
tương tự kẻ đường caoBK=> tam giác BKC vuông cân tại K
=> BK=KC
áp dụng Pitago =>BK=KC=4cm
ta có AB//DC ,BK vuông góc với DC=> AB vuông góc với BK
tứ giác ABKH có góc ABK=góc BKH=góc KHA=90 độ
=> T/g ABKH là hcn=> AB=HK=CD-(DH+KC)=14-(4+4)=6m
S ABCD=(AB+CD).AH:2=(6+14).4:2=40 cm vuông
Đúng 0
Bình luận (0)
Câu 1: Cho hình thang cân ABCD (AB//CD), AB=26cm , CD=10cm . AC vuông góc với BC. Tính diện tích hình thang đó.
Câu 2: Một hình thang cân có đường chéo vuông góc với cạnh bên. Tính chu vi và diện tích hình thang đó, biết rằng đáy nhỏ dài 14cm , đáy lớn dài 50cm
Cho hình thang ABCD có đáy CD=14cm.; cạnh bên AD=\(\sqrt{32}\)cm và góc ADC=45o. Diện tích hình thang cân ABCD là?
Bài 1:Tính chiều cao hình thang cân ABCD biết cạnh bên AD=5cm,cạnh đáy AB=6cm và CD=14cm
Bài 2: cho hình thang cân ABCD có I là giao điểm của 2 đường chéo.Chứng minh:IC=ID,IA=IB
Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, cạnh đáy AB = 6cm và CD = 14cm.
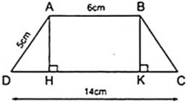
Kẻ AH ⊥ CD, BK ⊥ CD thì AH//BK nên hình thang ABKH có hai cạnh bên song song.
Áp dụng tính chất của hình thang ABKH có hai cạnh bên song song, ta có: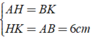
Áp dụng định lí Py – ta – go vào tam giác ADH vuông tại H ta được:
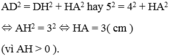
Vậy chiều cao của hình thang cân là 3cm.
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD ( AB//CD, AB<CD) biết AB=8cm, CD=14cm, AD=5cm. Tính đường cao AH của hình thang cân
kẻ 1 đg vuông góc từ B cắt DC tại K
xét tg ADH và tg BCK :
góc AHD= góc BKC ( = 90 độ )
AD= BC ( gt )
góc ADH= góc BCK ( gt )
=> tg ADH= tg BCK ( ch- gn)
=> DH= KC ( 2 cạnh t/ứ ) ( 1)
vì AB song song DC=> ABKD là hcn ( tự chứng minh)
=> AB=Dk= 8 cm
=> DH= KC= (DC-DK ) :2= 3 cm
áp dụng đlí pi-ta-go cho tg ADH vuông ở H :
AH2+DH2= AD2
TS : AH2= 52-32
=> AH = 4 cm
Đúng 0
Bình luận (0)
















