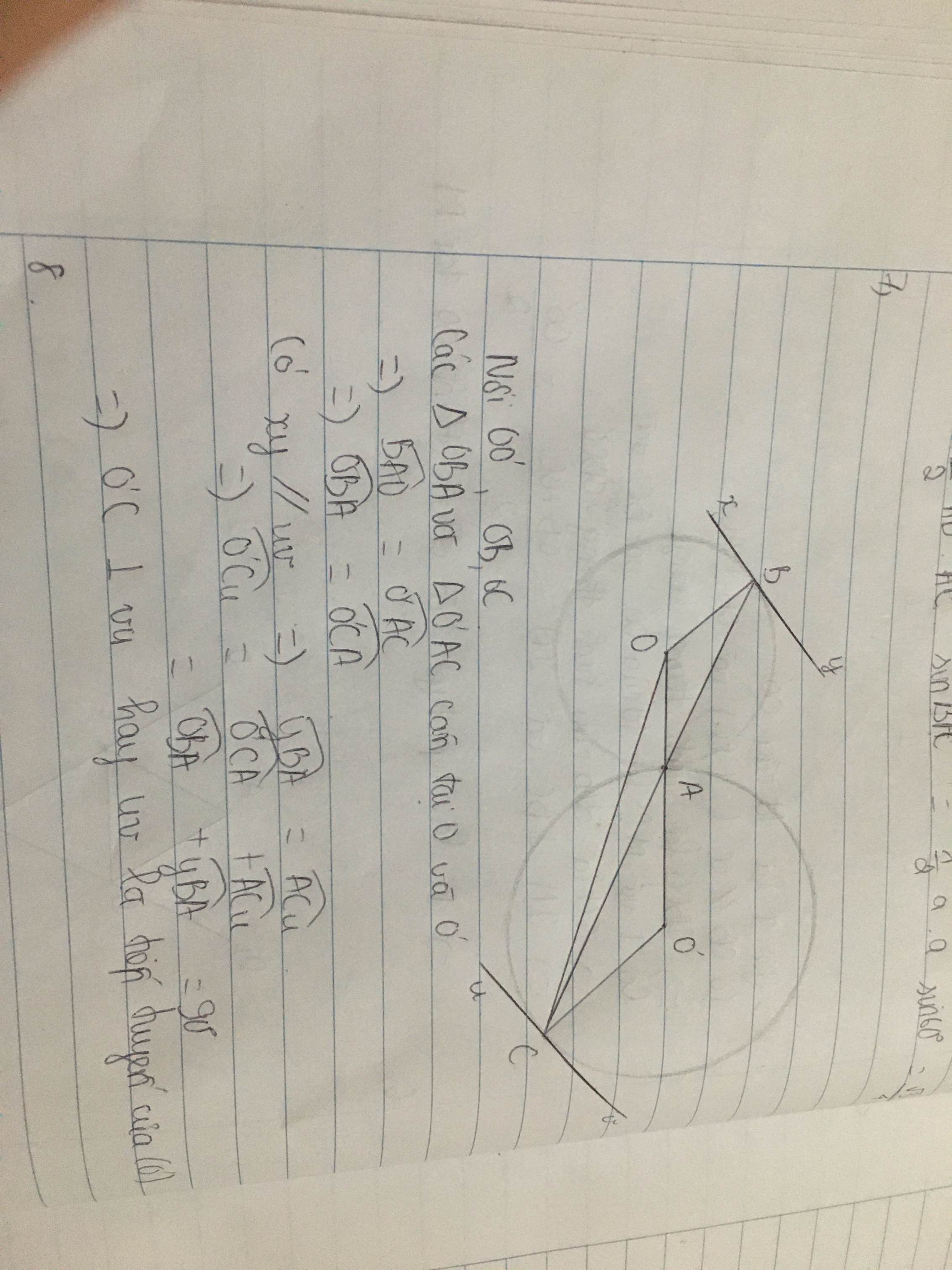Đường thẳng xy cắt đường tròn (O;7) tại 2 điểm.Khoảng cách d từ O đến xy thuộc khoảng [a;b). Vậy b =

Những câu hỏi liên quan
Cho đường thẳng xy đi qua điểm A nằm trong đường tròn (O; R). Chứng minh đường thẳng xy và đường tròn (O; R) cắt nhau
Kẻ OH vuông góc với xy suy ra OH ≤ OA . Mặt khác A nằm trong đường tròn (O;R) nên OA ≤ R
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và đường thẳng xy không có điểm chung với đường tròn. Lấy một điểm A bất kì thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Qua B kẻ đường thẳng vuông góc với AO, cắt AO tại K và cắt đường tròn (O) tại điểm thứ hai là C.
b. Chứng minh rằng: AC là tiếp tuyến của đường tròn (O).
c. Kẻ OH vuông góc với xy tại H, BC cắt OH tại I. Chứng minh rằng khi A di chuyển trên đường thăng xy thì độ dài đoạn thắng OI không đổi.
Đọc tiếp
Cho đường tròn (O; R) và đường thẳng xy không có điểm chung với đường tròn. Lấy một điểm A bất kì thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Qua B kẻ đường thẳng vuông góc với AO, cắt AO tại K và cắt đường tròn (O) tại điểm thứ hai là C. b. Chứng minh rằng: AC là tiếp tuyến của đường tròn (O). c. Kẻ OH vuông góc với xy tại H, BC cắt OH tại I. Chứng minh rằng khi A di chuyển trên đường thăng xy thì độ dài đoạn thắng OI không đổi.
cho đường thẳng xy đi qua điểm A nằm trong đường tròn (0;R). Chứng minh đường thẳng xy và đừng tròn (O;R)cắt nhau
Tham khảo:
Kẻ OH vuông góc với xy suy ra OH ≤ OA . Mặt khác A nằm trong đường tròn (O;R) nên OA ≤ R
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và đường thẳng xy cách tâm O một khoảng OKa(0aR). Từ một điểm A thuộc xy (OAR), vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm ; O và B nằm cùng phía với xy)a. Chứng minh đường thẳng xy cắt đường tròn (O) tại hai điểm D và Eb. Chứng minh 5 điểm O ,A, ,B, C, K cùng nằm trên một đường tròn. Xác định tâm của đường tròn nàyc.BC cách OA và OK theo thứ tự tại M và S. Chứng minhtuws giác AMKS nội tiếp được trong một đường tròn
Đọc tiếp
Cho đường tròn (O;R) và đường thẳng xy cách tâm O một khoảng OK=a(0<a<R). Từ một điểm A thuộc xy (OA>R), vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm ; O và B nằm cùng phía với xy)
a. Chứng minh đường thẳng xy cắt đường tròn (O) tại hai điểm D và E
b. Chứng minh 5 điểm O ,A, ,B, C, K cùng nằm trên một đường tròn. Xác định tâm của đường tròn này
c.BC cách OA và OK theo thứ tự tại M và S. Chứng minhtuws giác AMKS nội tiếp được trong một đường tròn
Cho đường tròn (O) bán kính R và đường thẳng xy không có điểm chung với đường tròn. Lấy A bất kì thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O). Qua B kẻ đường thẳng vuông góc AO tại K cắt đường tròn O tại điểm thứ 2 là C.a. Tính OK? nếu R 5cm, OA 10cmb. CMR: OC là tiếp tuyến đường tròn Oc. Kẻ OH vuông góc xy tại H. BC cắt OH tại y. CMR: Khi A di chuyển trên đường thẳng xy thì độ dài OI không đổi.
Đọc tiếp
Cho đường tròn (O) bán kính R và đường thẳng xy không có điểm chung với đường tròn. Lấy A bất kì thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O). Qua B kẻ đường thẳng vuông góc AO tại K cắt đường tròn O tại điểm thứ 2 là C.
a. Tính OK? nếu R= 5cm, OA= 10cm
b. CMR: OC là tiếp tuyến đường tròn O
c. Kẻ OH vuông góc xy tại H. BC cắt OH tại y. CMR: Khi A di chuyển trên đường thẳng xy thì độ dài OI không đổi.
1) Cho đường tròn
O R;
và đường thẳng xy. Chứng minh rằng nếu xy cắt đường tròn
O
tại hai điểm A và
B thì mọi điểm nằm giữa A, B đều nằm trong đường tròn
O
; mọi điểm còn lại trên xy (trừ A và B) đều nằm
ngoài đường tròn
O . giúp mik vs ạ
Kẻ OH vuông góc với xy suy ra OH ≤ OA . Mặt khác A nằm trong đường tròn (O;R) nên OA ≤ R
Đúng 1
Bình luận (4)
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE2. Cho tứ giác ABCD có AB BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh: a) tứ giác AQRC nội tiếp được 1 đường tròn b) QR//AD
Đọc tiếp
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Ta có: tỨ giác OCEA nội tiếp
=> \(\widehat{OCA}=\widehat{OEA}\)(1)
Vì OC=OB
=> Tam giác OBC cân
=> \(\widehat{OCA}=\widehat{OCB}=\widehat{OBC}\)(2)
Tứ giác ODAB nội tiếp
=> \(\widehat{ODA}=\widehat{OBC}\)( cùng bù với góc OBA) (3)
Từ (1), (2), (3)
=> \(\widehat{ODA}=\widehat{OEA}\)
=> Tam giác ODE cân có OA là đươngcao
=> OA là đường trung tuyến
=> A là trung điểm của DE
Đúng 0
Bình luận (0)
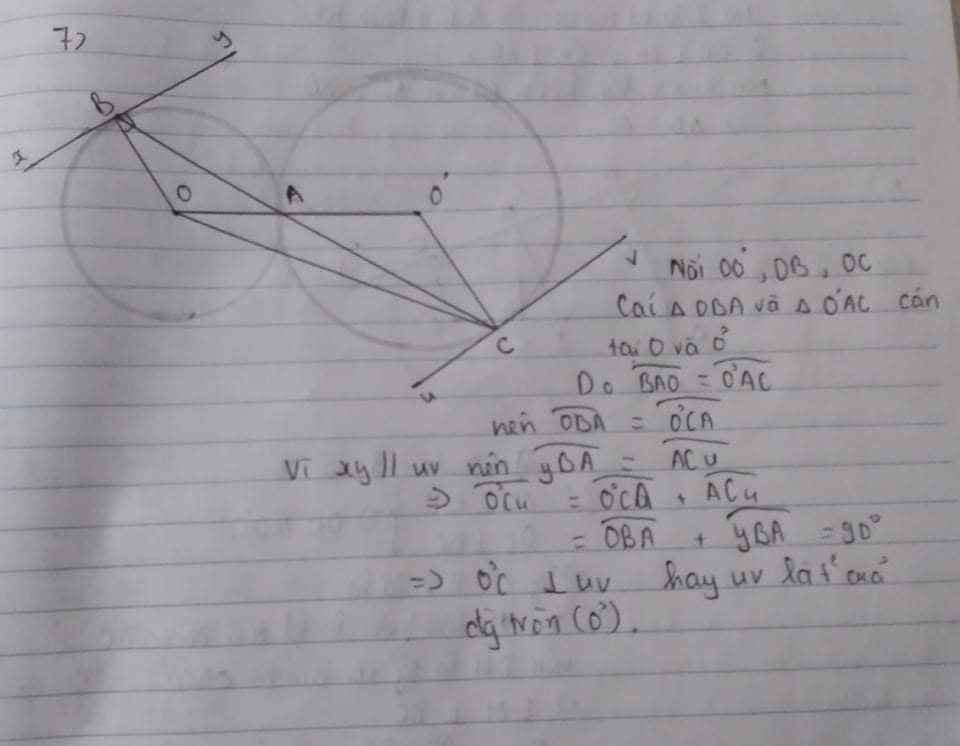
Cho hai đường tròn $(O)$ và $(O)$ tiếp xúc ngoài với nhau tại $A$. Qua $A$ vẽ một cát tuyến cắt đường tròn $(O)$ tại $B$ và cắt đường tròn $(O)$ tại $C$. Từ $B$ vẽ tiếp tuyến $xy$ với đường tròn $(O)$. Từ $C$ vẽ đường thẳng uv song song với đường thẳng xy. Chứng minh rằng uv là tiếp tuyến của đường tròn $(O)$.
Đọc tiếp
Cho hai đường tròn $(O)$ và $(O')$ tiếp xúc ngoài với nhau tại $A$. Qua $A$ vẽ một cát tuyến cắt đường tròn $(O)$ tại $B$ và cắt đường tròn $(O')$ tại $C$. Từ $B$ vẽ tiếp tuyến $xy$ với đường tròn $(O)$. Từ $C$ vẽ đường thẳng \(uv\) song song với đường thẳng \(xy\). Chứng minh rằng \(uv\) là tiếp tuyến của đường tròn $(O')$.
Xem thêm câu trả lời
Cho đường tròn (O) và đường thẳng xy tiếp xúc với đường tròn tại A. Vẽ đường tròn (I) đường kính OA.
a) Chứng minh rằng hai đường tròn (O) và (I) tiếp xúc với nhau
b) Vẽ dây cung AC của (O) cắt I tại một điểm thứ hai là M. Chứng minh MA=MC
c) đường thẳng OM cắt xy tại B. Chứng minh rằng BC là tiếp tuyến của (O)
Trên đường thẳng xy lấy một điểm O. Vẽ đường tròn (O;3cm) cắt Ox, Oy theo thứ tự tại A, B. Vẽ đường tròn (O;2cm) cắt Ox, Oy theo thứ tự tại C, D. Vẽ đường tròn (D;DB) cắt BO tại M và cắt đường tròn (O;2cm) tại N. So sánh AC, BD.