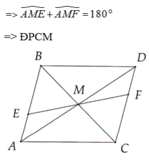
cho tam gaics ABC trên cạnh AB,AC lần lượt lấy các điểm M,N sao cho MA/MB=x; NA/NC=y. I = CM giao với BN. CMR vecto AI=x(vecto IB)+y(vecto IC)

Những câu hỏi liên quan
Cho tam giác ABC. Trên cạnh AB lấy điểm M sao cho MA bằng 2 lần MB; trên cạnh Ac lấy điểm N sao cho AN bằng 2 lần NC. Nối M với N ta được tam giác AMN có diện tích bằng 120 xăng-ti-mét vuông. Tính diện tích hình tam giác ABC.
Đáp án :180 cm2
Vì AM = 2/3 AB và AN = 2/3 AC nên SAMN = 2/3 AABC
Suy ra diện tích tam giác ABC sẽ là 180 cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC có diện tích 24cm2. Trên cạnh AB, BC lần lượt lấy M,N sao cho MA = MB: BC = 3 * BN. Trên đường kéo dài của đoạn thẳng AC lấy P sao cho AC = 4 * CP. Tính diện tích tam giáp MNP.
1,Cho tam giác ABC có diện tích bằng 175.5cm2.Trên đáy BC lấy điểm M sao cho BM2MC.Tính diện tích tam giác ABM và ACM2,Cho tam giác ABC có diện tích bằng 600cm2.Trên các cạnh BC;AB;AC lấy các điểm D;M;N sao cho BDDC;MAMB;NANC.Tính diện tích hình tam giác CMN?3,Cho tam giác ABC có diện tích bằng 400cm2.Trên các cạnh BC;CA lấy điểm M và N sao cho BMMC;ANNC.Tính diện tích tam giác CMN?4,Cho tam giác ABC có diện tích bằng 450cm2.Trên cạnh BC;CA lấy điểm M và N sao cho MC2BM;NANC.Tính diện tích tam g...
Đọc tiếp
1,Cho tam giác ABC có diện tích bằng 175.5cm2.Trên đáy BC lấy điểm M sao cho BM=2MC.Tính diện tích tam giác ABM và ACM
2,Cho tam giác ABC có diện tích bằng 600cm2.Trên các cạnh BC;AB;AC lấy các điểm D;M;N sao cho BD=DC;MA=MB;NA=NC.Tính diện tích hình tam giác CMN?
3,Cho tam giác ABC có diện tích bằng 400cm2.Trên các cạnh BC;CA lấy điểm M và N sao cho BM=MC;AN=NC.Tính diện tích tam giác CMN?
4,Cho tam giác ABC có diện tích bằng 450cm2.Trên cạnh BC;CA lấy điểm M và N sao cho MC=2BM;NA=NC.Tính diện tích tam giác CMN?
5,Cho tam giác ABC có diện tích bằng 360cm2.Trên các cạnh AB và AC lấy các điểm M và N sao cho MA=MB;NC=2NA.Tính diện tích tam giác AMN?
cho tam giác ABC có góc BAC = 40, trên cạnh AB,AC lần lượt lấy các điểm D và E sao cho BD = EC. Gọi M là trung điểm của DE, trên tia đối của tia MB lấy P sao cho MB = MP. Tính góc PCE
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
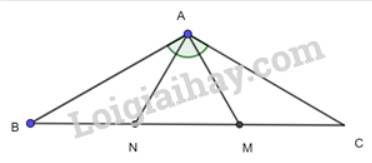
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.
Đúng 0
Bình luận (0)
Trên các cạnh AB, BC, AC của tam giác ABC lần lượt lấy các điểm M, N, P sao cho AM : MB = BN : NC = PC : PA.
a)Tính tỉ số Smnp/Sabc
b)Tìm tỉ số sao cho S tam giác MNP = 28% S tam giác ABC
Cho tam giác ABC có góc BAC=40 độ. Trên cạnh AB,AC lần lượt lấy các điểm D, E sao cho BD =DE. Gọi M là trung điểm của DE, trên tia đối của tia MB lấy P sao cho MB = MP. Tính góc PCE
Cho tam giác ABC, gọi M là trung điểm cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh AB = CD và AB //CD.
b) Chứng minh BD// AC.
c) Chứng minh ∆ A B C = ∆ D C B .
d) Trên các đoạn thẳng AB,CD lần lượt lấy các điểm E, F sao cho AE = DF. Chứng minh, ba điểm E, M, F thẳng hàng.
CHO TAM GIÁC ABC CÓ S BẰNG 360CM2. TRÊN CẠNH AB, AC LẤY ĐIỂM M,N SAO CHO MA=MB;NC=2NA. TÍNH S TAM GIÁC AMN