Cho hình hộp ABCD. A’B’C’D’ có tất cả các mặt đều là hình vuông cạnh a. Các điểm M; N lần lượt trên AD’ và BD sao cho AM= DN= x. Khi x = a 2 3 thì MN song song với đường thẳng nào?
A. A’C
B. AC
C. B’A
D. Đáp án khác
Cho hình hộp A B C D . A ' B ' C ' D ' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A ' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. V = 4 a 3 2 3
B. V = 4 a 3 2
C. V = 8 a 3
D. V = 8 a 3 3
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu của đỉnh A' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. V = 4 2 a 3 3
B. V = 8 2 a 3
C. V = 8 a 3 3
D. V = 8 a 3 3
Chọn B

Ta có: A'O ⊥ (ABCD); OA= A C 2 = a 2
A ' O = A A ' 2 - O A 2 = a 2
V A B C D . A ' B ' C ' D ' = S A B C D . A ' O = 4 a 2 . a 2 = 4 2 a 3
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và B A D ^ = B A A ' ^ = D A A ' ^ = 60 ° . Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
A. a 5 5
B. a 6 3
C. a 10 5
D. a 3 3
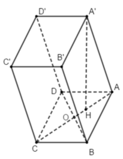
+ Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD
Ta có: A’B = A’D (đường chéo các hình thoi) ⇒ Tam giác A’BD cân tại A’ có O là trung điểm của BD ⇒ A’O ⊥ BD.
+ Hạ A’H ⊥ AC, H ∈ AC
Ta có B D ⊥ A C B D ⊥ A ' O ⇒ B D ⊥ A O A ' ⇒ A’H ⊥ BD
Do đó: A’H ⊥ (ABCD)
Vì (ABCD) // (A’B’C’D’) nên A’H chính là khoảng cách giữa hai mặt đáy.
+ Tính A’H
Ta có: AC = A D 2 + C D 2 − 2. A D . C D . cos 120 ° = a 3 ⇒ AO = a 3 2
Theo giả thiết ⇒ hình chóp A’.ABD là hình chóp đều, nên ta có:
AH = 2/3 AO = a 3 3
A’H = A ' A 2 − A H 2 = a 2 − a 2 3 = a 6 3
Vậy khoảng cách giữa hai đáy (ABCD) và (A’B’C’D’) là a 6 3 .
Đáp án B
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh , BD = 3a, hình chiếu vuông góc của B lên mặt phẳng (A’B’C’D’) là trung điểm của A’C’. biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD’C’) bằng 21 7 . Tính theo a thể tích khối hộp ABCD.A’B’C’D’
A. 9 a 3 4
B. a 3
C. 9 a 3 2
D. 3 a 3 2
Hình hộp chữ nhật có …… mặt, …… cạnh, …… đỉnh
b) Tất cả các mặt của hình hộp chữ nhật là hình ……………………………
c) Hình lập phương có …… mặt, …… cạnh, …… đỉnh
d) Tất cả các cạnh của hình lập phương đều có độ dài ………………………
e) Tất cả các mặt của hình lập phương đều là hình ……………………………
a) HÌNH HỘP CHỮ NHẬT CÓ 6 MẶT , 12 CẠNH, 8 ĐỈNH .
b) TẤT CẢ CÁC MẶT CỦA HÌNH HỘP CHỮ NHẬT ĐỀU LÀ HÌNH CHỮ NHẬT .
c) HÌNH LẬP PHƯƠNG CÓ 6 MẶT ,12 CẠNH , 8 ĐỈNH .
d) TẤT CẢ CÁC MẶT CỦA HÌNH LẬP PHƯƠNG ĐỀU CÓ ĐỘ DÀI GIỐNG NHAU .
e) TẤT CẢ CÁC MẶT CỦA HÌNH LẬP PHƯƠNG ĐỀU LÀ HÌNH VUÔNG.
HẾT ................................................ .
Cho hình chóp S. ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông. Gọi M là trung điểm của CD. Giá trị M S → . C B → bằng
A. a 2 2
B. - a 2 2
C. a 2 3
D. 2 a 2 2
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , hình chiếu vuông góc của B lên mặt phẳng (A’B’C’D’) là trung điểm của A’C’. Biết rằng côsin của góc tạo bởi hai mặt phẳng (ABCD) và (CDD’C’) bằng 21 7 . Tính theo a bán kính mặt cầu ngoại tiếp tứ diện A’BC’D’.
A. a
B. 2a
C. 3a
D. a 2
Cho hình lập phương ABCD. A’B’C’D’ cạnh a. Gọi N là trung điểm của cạnh CC’. Mặt phẳng (NAB) cắt hình hộp theo thiết diện là hình chữ nhật có chu vi là:
![]()
![]()
![]()
D. Cả A, B, C đều sai
Cho hình hộp ABCD.A'B'C'D' tất cả các cạnh đều bằng a, góc BAD = 60 độ, hình chiếu vuông góc của A' xuống (ABCD) trùng với trung điểm của AB. Tính thể tích khối hộp ABCD.A'B'C'D'.