Gọi G là trọng tâm của tam giác ABC.Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) CMR:BG'=CG
b)Đường trung trực của BC lần lượt cắt AG;AC;GC và BG' tại I;J;K
c)CMR:Góc ICJ=IBJ
Bài 3: Cho tam giác nhọn ABC. Gọi H,G,O lần lượt là trực tâm , trọng tâm giao điểm ba đường trung trực của tam giác do. tia AG cắt BC ở M. Gọi I là trung điểm cua GA, K là trung điểm của GH. Chứng minh
a) OM=1/2 AH
b) Tam giác IGK= Tam giác MGO
c) Ba điểm H,G,O thẳng hàng
d) GH = 2GO
a/
O là giao 3 đường trung trực nên O là tâm đường tròn ngoại tiếp tg ABC
Nối AO cắt đường trong (O) tại E ta có
\(\widehat{ABE}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow BE\perp AB\)
H là trực tâm tg ABC \(\Rightarrow CH\perp AB\)
=> BE//CH (1)
Ta có
\(\widehat{ACE}=90^o\) (Góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow CE\perp AC\)
H là trực tâm tg ABC \(\Rightarrow BH\perp AC\)
=> CE//BH (2)
Từ (1) và (2) => BHCE là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Do trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường mà G là trọng tâm tg ABC => M là trung điểm BC => M cũng là trung điểm của HE => MH = ME
Xét tg AHE có
MH=ME (cmt)
OA=OE
=> OM là đường trung bình của tg AHE \(\Rightarrow OM=\dfrac{1}{2}AH\)
b/
Ta có M là trung điểm của BC (cmt) => OM là đường trung trực của BC \(OM\perp BC\)
\(AH\perp BC\)
=> OM//AH
Xét tg AGH có
IA=IG (gt)
KH=KG (gt)
=> IK là đường trung bình của tg AGK => IK//AH mà OM//AH (cmt)
=> IK//OM \(\Rightarrow\widehat{GIK}=\widehat{GMO}\) (góc so le trong) (4)
IK là đường trung bình của tg AGH \(\Rightarrow IK=\dfrac{1}{2}AH\) mà \(OM=\dfrac{1}{2}AH\) (cmt) => IK = OM (5)
G là trong tâm tg ABC => \(GM=\dfrac{1}{2}AG\) mà \(IG=\dfrac{1}{2}AG\)
=> IG=GM (6)
Từ (4) (5) (5) => tg IGK = tg MGO (c.g.c)
c/
Nối H với O cắt AM tại G' Xét tg AHE
MH=ME (cmt) => AM là trung tuyến của tg AHE
OA=OE => HO là trung tuyến của tg AHE
=> G' là trọng tâm của tg AHE \(\Rightarrow G'M=\dfrac{1}{3}AM\)
Mà G là trọng tâm của tg ABC \(\Rightarrow GM=\dfrac{1}{3}AM\)
\(\Rightarrow G'\equiv G\) => H; G; O thẳng hàng
d/
Do G là trọng tâm của tg AHE => GH=2GO
bài 2: gọi G là trọng tâm của tam giác ABC.trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a)so sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC
b) so sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
a) Ch/m BG'=CG
b) Đ ường trung trực của cạnh BC cắt AC,CG,BG' lần lược tại I,J,K.Ch/m BK=CJ
c) Ch/m ICJ=IBJ
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'
So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC.
Gọi I, K lần lượt là trung điểm của BG, BG’.
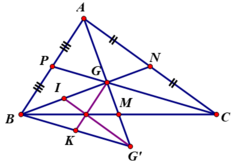
* M là trung điểm GG’⇒ BM là đường trung tuyến ΔBGG.
Mà M là trung điểm BC ⇒ BM = ½ .BC (4)
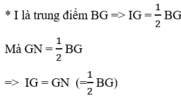
Xét ΔIGG’ và ΔNGA có:
IG = GN (chứng minh trên)
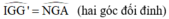
GG’ = GA (Vì G là trung điểm AG’)
⇒ ΔIGG’ = ΔNGA (c.g.c)
⇒ G’I = AN (hai cạnh tương ứng)
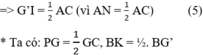
Mà GC = BG’ (chứng minh phần a))
⇒ Nên PG = BK.
ΔGMC = ΔG’MB (chứng minh câu a)

Xét ΔPGB và ΔKBG có:
PG = BK (chứng minh trên)
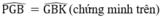
BG chung
⇒ ΔPGB = ΔKBG (c.g.c)
⇒ PB = GK (hai cạnh tương ứng)
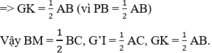
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
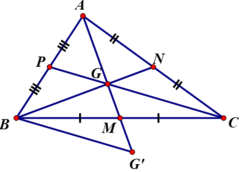
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
⇒ AM, BN, CP là các đường trung tuyến, G là trọng tâm của ΔABC
Theo tính chất đường trung tuyến của tam giác ta có:
GB = 2/3.BN (1)
GA = 2/3.AM, mà GA = GG’ (do G là trung điểm của AG’) ⇒ GG’ = 2/3.AM (2)
GM=1/2.AG, mà AG=GG’ ⇒ GM=1/2.GG’ ⇒ M là trung điểm của GG’ hay GM = G'M .
Xét ΔGMC và ΔG’MB có:
GM = G’M (chứng minh trên)
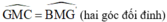
MC = MB
⇒ ΔGMC = ΔG’MB (c.g.c)
⇒ GC = G’B (hai cạnh tương ứng).
Mà CG = 2/3.CP (tính chất đường trung tuyến) ⇒ G’B = 2/3.CP (3)
Từ (1), (2), (3) ta có : GG’ = 2/3.AM , GB = 2/3.BN, G’B = 2/3.CP.
Cho tam giác ABC(AB<AC) và AM là trung tuyến. Gọi G là trọng tâm của tam giác ABC, trên tia AM lấy điểm G' sao cho G là trung điểm của AC'
a) Chứng minh MG' = \(\frac{1}{2}\)AG
b) Chứng minh BG'=GC
c)Đường trung trực của cạnh BC lần lượt cắt các cạnh AC,Cg tại I và k. Chứng minh tam giác ICK = tam giác IBK
Hình như là điểm C đó cậu.Chắc mình gõ nhầm
Cho tam giác ABC. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F
sao cho BE = CF.
a) Chứng minh rằng 2 tam giác ABC và AEF có cùng trọng tâm (gọi trọng tâm chung đó là G)
b) AG cắt BC tại M. Gọi H là trung điểm AG, Nối EG cắt AF tại N. Lấy I là trung điểm EG.
Chứng minh IH // MN và IH = MN
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'. So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
1, Cho tam giác ABC. Lấy P nằm trong tam giác sao cho ^PAC=^PBC. Gọi M và N lần lượt là hình chiếu của điểm P trên AC và BC. Gọi D,E,F lần lượt là trùg điểm của AB,AP,BP. CM: ∆MED=∆DFN
2, cho ∆ABC. Gọi H, G, O theo thứ tự là trực tâm, trọng tâm,giao điểm ba đường trung trực của tam giác. Tia AG cắt BC ở M. Gọi I là trung điểm của GA, K là trung điểm của GH. Cm:
a, OM=1/2 AH
b, ∆IAK=∆MGO
c, ba điểm H,G,O thẳng hàng
d, GH=2GO
Giải hộ nha!!!!!Thanks