Xét ΔABC có

D là trung điểm của AB

F là trung điểm của AC

Do đó: DF là đường trung bình của ΔABC

Suy ra: \(DF=\dfrac{BC}{2}\)

Xét ΔABC có

D là trung điểm của AB

E là trung điểm của BC

Do đó: DE là đường trung bình của ΔBAC

Suy ra: \(DE=\dfrac{AC}{2}\)

Xét ΔACB có

F là trung điểm của AC
E là trung điểm của BC

Do đó: FE là đường trung bình của ΔACB

Suy ra: \(FE=\dfrac{AB}{2}\)

Ta có: \(C_{DEF}=DF+DE+EF\)

\(=\dfrac{AB+AC+BC}{2}\)

\(=\dfrac{C_{ABC}}{2}\)

a)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các cặp cạnh tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) BC = EF
\(\Rightarrow\) BM = EN (vì BM = BC/2, EN = EF/2 (1)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các góc tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) Góc ABC = EFBC = góc DEF (2)
+ Có hai tam giác ABC và tam giác DEF bằng nhau nên các cặp cạnh tương ứng của hai tam giác bằng nhau.
\(\Rightarrow\) AB = DE
+ Xét hai tam giác BAM và tam giác DEN, ta có:
\(\left\{{}\begin{matrix}BM=EM\\\widehat{ABC}=\widehat{DEF}\\AB=DE\end{matrix}\right.\)
nên hai tam giác BAM và tam giác DEN bằng nhau theo trường hợp cạnh - góc - cạnh.
b)
+ Có \(\left\{{}\begin{matrix}\Delta ABC=\Delta DEF\\\Delta ABM=\Delta DEN\end{matrix}\right.\)
nên \(\Delta ABC-\Delta ABM=\Delta DEF-\Delta DEN\)
\(\Rightarrow\) Hai tam giác AMC và tam giác DNF bằng nhau.
\(\Rightarrow\) Hai góc MAC và góc NDF tương ứng bằng nhau.

Mong cái này giúp được bạn nhé. ☺

xét 2 tam giác vuông ABC và tam giác EDF, ta có: 
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF 
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)

Cho tam giác ABC và tam giác DEF có: AB=DE,BC=EF,AC=DF.

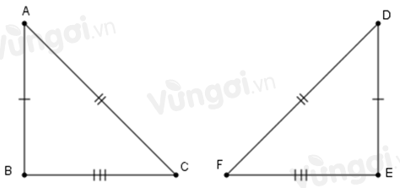
Xét ΔABC và ΔDEF có:

AB=DE(gt)

BC=EF(gt)

AC=DF(gt)

⇒ΔABC=ΔDEF (c.c.c).

Học tốt nhé!

a/ Ta có: \(\widehat{B}\)=\(\widehat{F}\); AB = EF

Để tam giác ABC = tam giác DEF theo trường hợp cạnh góc cạnh, ta cần bổ sung điều kiện BC = FD

Khi đó. tam giác ABC = tam giác EFD (c.g.c)

b/ Ta có: tam giác ABC = tam giác EFD

=> AB = EF; BC = FD; AC = DE

Chu vi tam giác ABC = tam giác EFD

AB + BC + AC = EF + FD + DE = 5 + 6 + 6

= 17 (cm)

Vậy chu vi tam giác ABC=chu vi tam giác EFD = 17 cm