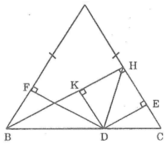
Bài 4: Cho tam giác ABC (AB = AC), đường cao BH. Từ điểm D thuộc cạnh BC kẻ DE ⊥ AB (E ∈ AB); DF ⊥ AC (F ∈ AC) và DK ⊥ BH (K ∈ BH)
a) Chứng minh: \(\widehat{KDB}=\widehat{ACB}\)
b) Chứng minh: ΔEBD = ΔKDB.
c) Chứng minh: DE + DF = BH.
d) Trên tia đối của tia CA lấy điểm P sao cho CP = HF. Chứng minh rằng trung điểm của EP nằm trên BC.
e) Cho \(\widehat{A}=40^o\), kẻ đường cao AH. Trên các đoạn thẳng AH, AC lấy thứ tự các điểm E, F sao cho \(\widehat{ABE}=\widehat{CBF}=30^o\). Tính góc AEF.