cho tam giác ABC vuông tại A. Phân giác góc B và góc C cắt nhau tại I. Gọi K là hình chiếu của I trên BC. Biết BK=a ; CK=b. Tính S tam giác ABC theo a;b

Những câu hỏi liên quan
1. cho tam giác ABC cân tại A ,có AM là tia phân giác của góc A(M thuộc BC).Kẻ BK vuông góc vs AC cắt AM tại I ( K thuộc AC)
a. Chứng minh CI vuông góc vs AB
b. lấy điểm D bất kí trên cạnh BC, gọi hình chiếu của D trên AB,AC và BK thứ tự là P,Q và H. Chứng minh BK=DP+DQ
a)
Ta có: ΔABC cân tại A(gt)
mà AM là đường phân giác ứng với cạnh đáy BC(gt)
nên AM là đường cao ứng với cạnh BC(Định lí tam giác cân)
\(\Leftrightarrow AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(cmt)
BK là đường cao ứng với cạnh AC(Gt)
AM cắt BK tại I(Gt)
Do đó: I là trực tâm của ΔBAC(Tính chất ba đường cao của tam giác)
Suy ra: CI\(\perp\)AB(Đpcm)
Đúng 0
Bình luận (0)

a) Tam giác ABC cân tại A có AM là phân giác, do đó AM cũng là đường cao
AM vuông góc với BC
Lại có BK vuông góc với AC
Do đó I là trực tâm của tam giác ABC
Vậy CI vuông góc với AB
b) Tam giác BDH = tam giác DBP (ch.gn)
Do đó BH = DP
BDKQ là hình chữ nhật => DP = HK
=> BK = BH + HK = DP + DQ (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, AB AC BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC, H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI AH. Gọi K là giao điểm của FH và AI. CM 3 điểm B,O,K thẳng hàngCho tam giác ABC nhọn, AB AC BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC, H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI AH. Gọi K là giao điểm của FH và AI. CM 3 điểm B,O,K thẳn...
Đọc tiếp
Cho tam giác ABC nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC, H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI. CM 3 điểm B,O,K thẳng hàngCho tam giác ABC nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC, H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI. CM 3 điểm B,O,K thẳng hàng
Cho tam giác ABC vuông tại A. Một điểm H di chuyển trên cạnh AB. K là hình chiếu của B trên CH. BK cắt AC tại I. a) CMR: IH vuông góc với BC. Gọi chân đường vuông góc là M
a: Xét ΔCIB có
CK,BA là đường cao
CK cắt BA tại H
=>H là trực tâm của ΔCIB
=>IH vuông góc BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Một điểm H di chuyển trên cạnh AB. K là hình chiếu của B trên CH. BK cắt AC tại I. a) CMR: IH vuông góc với BC. Gọi chân đường vuông góc là M
a: Xét ΔCIB có
CK,BA là đường cao
CK cắt BA tại H
=>H là trực tâm của ΔCIB
=>IH vuông góc BC
Đúng 0
Bình luận (0)
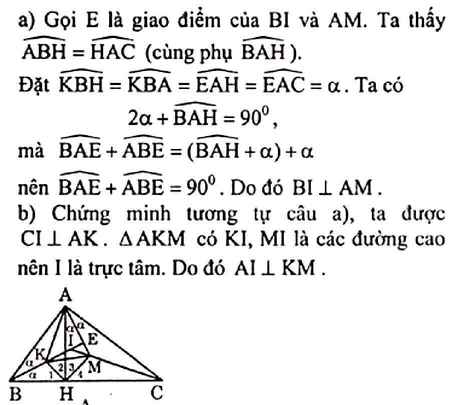
Cho tam giác ABC vuông tại A, H là hình chiếu của A trên BC. Các tia phân giác của góc B và C cắt nhau tại I. Tia phân giác của góc AHB cắt BI ở K. Tia phân giác của góc AHC cắt CI ở M. Chứng minh rằng:
a/ BI vuông góc với AM.
b/ AI vuông góc với KM.
Nhanh giúp mình với ạ, vẽ cả hình được nữa thì càng tốt ạ
1. cho tam giác ABC cân tại A ,có AM là tia phân giác của góc A(M thuộc BC).Kẻ BK vuông góc vs AC cắt AM tại I ( K thuộc AC)
a. Chứng minh CI vuông góc vs AB
b. lấy điểm D bất kí trên cạnh BC, gọi hình chiếu của D trên AB,AC và BK thứ tự là P,Q và H. Chứng minh BK=DP+DQ
a: Xét ΔABC có
AM,BK là đường cao
AM cắt BK tại I
=>I là trực tâm
=>CI vuông góc AB tại N
b:
Xet ΔAKB vuông tại K và ΔANC vuông tại N có
AB=AC
góc KAB chung
=>ΔAKB=ΔANC
=>BK=CN
DP//NC
=>DP/NC=BD/BC
=>DP/BK=BD/BC
DQ//BK
=>DQ/BK=CD/CB
=>DQ+DP=BK(BD/BC+CD/CB)=BK
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại B. Qua A kẻ đường thẳng vuông góc với AB,qua C kẻ đường vuông góc CB, chúng cắt nhau tại K. chứng minh rằng:
a, Bk là tí phân giác của góc B
b,Gọi I là giao điểm của AC và BK. C/m AC vuông BK
Biết BC là 10cm và AC là 6 tính BI
Xem chi tiết
a) Xét ΔBAK vuông tại A và ΔBCK vuông tại C có
BK chung
BA=BC(ΔBAC cân tại B)Do đó: ΔBAK=ΔBCK(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABK}=\widehat{CBK}\)(hai góc tương ứng)
mà tia BK nằm giữa hai tia BA,BC
nên BK là tia phân giác của \(\widehat{ABC}\)(đpcm)
b) Ta có: ΔBAK=ΔBCK(cmt)
nên KA=KC(Hai cạnh tương ứng)
Ta có: BA=BC(ΔABC cân tại B)
nên B nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có:KA=KC(cmt)
nên K nằm trên đường trung trực của AC(Tính chất đường trung trực của một đoạn thẳng) (2)
Từ (1) và (2) suy ra BK là đường trung trực của AC
hay BK\(\perp\)AC(đpcm)
Vì BK là đường trung trực của AC(cmt)
nên BK vuông góc với AC tại trung điểm của AC
mà BK cắt AC tại I(gt)
nên BK\(\perp\)AC tại I và I là trung điểm của AC
Ta có: I là trung điểm của AC(cmt)
nên \(CI=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBIC vuông tại I, ta được:
\(BC^2=BI^2+IC^2\)
\(\Leftrightarrow BI^2=BC^2-IC^2=10^2-3^2=91\)
hay \(BI=\sqrt{91}cm\)
Vậy: \(BI=\sqrt{91}cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, phân giác các góc B và C cắt nhau ở I, gọi H là hình chiếu của I trên BC. Giả sử BH = 5cm; CH = 7cm. Tính diện tích tam giác ABC.
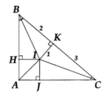
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI lcm, BK 2cm, KC 3cm.a) Chứng minh
∆
B
H
I
∆
B
K
I
b) Chứng minh tam giác AHI là tam giác vuông cân.c) Tính chu vi tam giác ABC.
Đọc tiếp
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = lcm, BK = 2cm, KC = 3cm.
a) Chứng minh ∆ B H I = ∆ B K I
b) Chứng minh tam giác AHI là tam giác vuông cân.
c) Tính chu vi tam giác ABC.