cho tam giác ABC có B = 120 độ , phân giác là BD;CE . Đường thẳng tia phân giác ngoài tại đỉnh A của tam giác ABC cắt BC tại F . Chứng minh rằng :a, góc ADF=góc BDF b, 3 điểm D,E,F thẳng hàng

Những câu hỏi liên quan
Cho tam giác ABC có góc B bằng 120 ° , BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D. Tính độ dài đường phân giác BD

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()
Đúng 0
Bình luận (0)
cho tam giác abc có góc b = 120 độ,phân giác bd;ce.đường chứa tia phân giác góc ngoài tại đỉnh a của tam giác abc cắt bc tại f.từ k kẻ fi,fk,fh lần lượt vuông góc với các đường thẳng bd,ba,ac.cmr:fi=fk=fh
cho tam giác abc có góc b = 120 độ,phân giác bd;ce.đường chứa tia phân giác góc ngoài tại đỉnh a của tam giác abc cắt bc tại f.từ k kẻ fi,fk,fh lần lượt vuông góc với các đường thẳng bd,ba,ac.cmr:fi=fk=fh
Cho tam giác ABC có góc B bằng 120 độ,BC = 12cm,AB = 6cm.Đường phân giác của góc B cắt cạnh AC tại D
a) Tính độ dài đường phân giác BD
b) Gọi M là trung điểm của BC.Chứng minh AM vuông góc với BD.
c) Tính AM và diện tích tam giác ABM
a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.
cho tam giác abc có góc b bằng 120 độ, bc = 12cm, AB=6cm. Đường phân giác của góc B cắt AC tại D.
a) tính đường phân giác BD.
b) M là trung điểm của BC. CHứng minh AM vuông góc với BD
Cho tam giác ABC có góc B= 120 độ, BC= 12 cm, AB=6cm,đường phân giác góc B cắt AD tại D.
a/ Tính BD
b/ Tính tỉ số diện tích của tam giác ABD và tam giác ABC
c/ Tính diện tích tam giác ABD, tam giác BCD
d/ M là trung điểm BC. Chứng minh: AM vuông góc BD
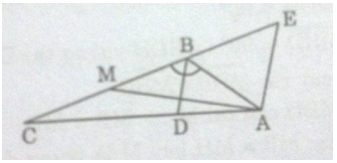
Cho tam giác ABC có góc B bằng 120∘120∘, BC = 12cm, AB = 6cm. đường phân giác của góc B cắt cạnh AC tại D.
a) Tính độ dài đường phân giác BD.
b) Gọi M là trung điểm của BC. Chứng minh AM⊥ BD.
.

a) Ta có:
ˆABD=ˆCBD=\(\frac{\widehat{ABC}}{2}\)=120∘: 2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘(so le trong)
ˆCBD=ˆAEB=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
\(\frac{BC}{CE}\)=\(\frac{DC}{AE}\)⇒BD=\(\frac{BC.AE}{CE}\)=\(\frac{12.6}{18}\)=4(cm)
b) Ta có:
MB=MC=\(\frac{1}{2}\).BC=\(\frac{1}{2}\).12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
tk mik nha
Đúng 1
Bình luận (0)
a) Ta có:
\(\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}=\frac{120^o}{2}=60^o\)
Từ A kẻ đường thẳng song song với BD cắt CB tại E
Lại có:
\(\widehat{BAE}=\widehat{ABD}=60^o\) ( so le trong )
\(\widehat{CBD}=\widehat{AEB}=60^o\) ( đồng vị )
Suy ra tam giác ABE đều
=> AB = BE = EA = 6 ( cm ) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 ( cm )
Tam giác ACE có AE // BD nên suy ra :
\(\frac{BC}{CE}=\frac{BD}{AE}\)
\(\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4\left(cm\right)\)
b) Ta có:
\(MB=MC=\frac{1}{2}.BC=\frac{1}{2}.12=6\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra:
BM = AB => Tam giác ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao ( tính chất tam giác cân )
Vậy \(BD\perp AM\)
Cho tam giác ABC,góc B= 120 độ,BC=12,AB=6.Phân giác góc B cắt AC tại D. Tính diện tích ABd
Cho tam giác abc với các đường cao ah, biết góc abc=120, ab=6,25cm, bc=12,5cm. Đường phân giác của góc b cắt ac tại d.
a) Tính độ dài bd
b) Tính tỷ số diện tích của tam giác abd và abc
c) Tính diện tích của tam giác ABD
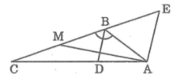
. Cho tam giác ABC có góc A=120 độ . Đường phân giác của góc B và góc C là BD và CE cắt nhau tại I.
a, Tính số đo của góc BIC.
b, Kẻ tia IA, hãy tính góc EAI.
c, Điểm I có cách đều ba cạnh của tam giác ABC hay không? Tại sao?
giúp mk vs:((
![]()
Bạn bổ sung đề đi bạn: Số đo của góc B và góc C là bao nhiêu???
Đúng 2
Bình luận (1)
a) Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=60^0\)
\(\Leftrightarrow2\left(\widehat{IBC}+\widehat{ICB}\right)=60^0\)
hay \(\widehat{IBC}+\widehat{ICB}=30^0\)
Xét ΔIBC có \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{BIC}+30^0=180^0\)
hay \(\widehat{BIC}=150^0\)
Vậy: \(\widehat{BIC}=150^0\)
Đúng 0
Bình luận (0)
c) Xét ΔABC có
BD là đường phân giác ứng với cạnh AC(gt)
CE là đường phân giác ứng với cạnh AB(gt)
BD cắt CE tại I(gt)
Do đó: I là tâm đường tròn nội tiếp ΔABC
hay I cách đều ba cạnh của ΔACB
Đúng 0
Bình luận (0)















