Tự vẽ hình nha=0

Ta có:

\(AC=\sqrt{\left(\dfrac{1}{2}CD\right)^2+\left(\dfrac{1}{2}AB\right)^2}=\sqrt{6^2+12^2}=6\sqrt{5}\left(cm\right)\)

\(R=\dfrac{OO'}{2}+\dfrac{CD}{2}\)

Mặt khác tứ giác `AOBO'` là hình thoi:

\(2R=OO'+CD=OO'+12\left(cm\right)\\ \Rightarrow R=10\left(cm\right)\)

`HaNa♫D`

a. b.

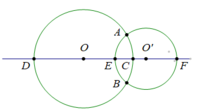
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB

Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm

- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB

Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm

d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.

Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m  

Mà EO’=1cm, nên OE=EO’ (=1cm)

Do đó: E là trung điểm của đợn thẳng OO’.

e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.

Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .

Vậy DF=4,5cm

Câu b.
Ta có tam giác EOH cân tại O
=> góc OEH=goc OHE
=> góc OHE= góc EHB (vì AHB cân Có HE là đường cao đồng thời là đường phân giác )
xét tứ giác EHDB nt
có gócEHB=gócEDB (cùng chắn EB)
=> góc OEH=gócEDB
Xét ttam giác EHD cân tại H ( H là  trực tâm trong tam giác ABC cân)
có góc HED=góc HDE 
mà góc HDE+gocEDB=90độ
=> góc HED+gocOEH=90độ
<=>OE vuông góc ED
câu c.
Xét tam giác BDA vuong tại D
AB²=AD²+DB² (pytago)
AD²=AB²-BD²
AD²=169-25
AD²⁼¹⁴⁴
AD=12
Xet tam giác OED vuông tại E có:
tam giác EHD cân => tam giác HEO cân  ( trong tam giác vuông đường trung tuyến là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện, sẽ chia ra 2 cạch = nhau )
Xét (O) có
O là trung điểm AH
=>OA=OH
Ta lại có H là trung điểm OD
do đó OA=OH=HD
mà AD=12
=>OA=OH=HD=12/3
=>OA=4cm

ko có câu a à bn