Hướng dẫn giải:

Diện tích hình thoi là:

     12 x 5 : 2 = 30 ( c m 2 )

       Đáp số: 30 c m 2 .

Đáp án B

Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..

Gọi O là tâm hình vuông.

Theo tính chất hình vuông ta có:

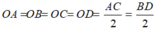
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

titititutut

Gọi \(O\) là giao điểm của \(AC\)và \(BD\).

Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)

Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)

Áp dụng định lí Pitago trong \(\Delta AOB\) có:

\(AB^2=AO^2+OB^2\)

\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)

\(\Rightarrow AB=5cm\)

\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)

Vậy ...............

Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)

\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)

\(\Rightarrow8a^2=32\)

\(\Rightarrow a^2=4\)

\(\Rightarrow a=2\left(cm\right)\)

Ta có: AC = 2AO = 2.12 = 24cm

S_ABCD =  1 2 BD.AC

=> BD = 2 S A B C D A C = 2.168 24 =14(cm)

=> BO =  1 2 BD = 1 2 .14 = 7(cm)

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)

Đáp án cần chọn là: C

Áp dụng công thức thay m, n zo công thức là xong, vì không cho độ dài nên kết quả là cái công thức sau khi đã thay m,n zo

Gọi O là giao điểm của 2 đường chéo của hình thoi

\(\Rightarrow\)O là trung điểm của AC và BD 

\(\Rightarrow OA=\frac{1}{2}AC=\frac{1}{2}.8=4\left(cm\right)\)và \(OB=\frac{1}{2}BD=\frac{1}{2}.6=3\left(cm\right)\)

Tứ giác ABCD là hình thoi \(\Rightarrow AC\perp BD\)\(\Rightarrow OA\perp OB\)\(\Rightarrow\Delta OAB\)vuông tại O

Áp dụng định lý Pytago ta có: \(OA^2+OB^2=AB^2\)

\(\Rightarrow AB^2=4^2+3^2=16+9=25\)\(\Rightarrow AB=5\left(cm\right)\)

Vì ABCD là hình thoi \(\Rightarrow AB=BC=CD=CA\)

\(\Rightarrow P_{ABCD}=4.AB=4.5=20\left(cm\right)\)

 \(S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot8\cdot16=64\left(cm^2\right)\)

Nhầm, dòng thứ 2 từ dưới lên phải là \(AB=BC=CD=DA\)

chuc mung nam moi

mk đang lam đoi xiu

vi ac=12cm nên ab=12cm.

vibd=6cm nên cd=6cm

chu vi hinh thoi la 

12x2cong6x2=36cm

đap so 36 cm