Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
A. 0; 3
B. 2; 4
C. 0; 2
D. 1; 3
Cho hàm số y= 2x3-3( m+ 1) x2+ 6mx+ m3 với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực trị A; B thỏa mãn AB = 2
A. m=0
B. m=0; m= 2.
C. m=1
D. m=2
Ta có
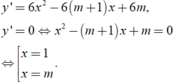
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
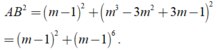
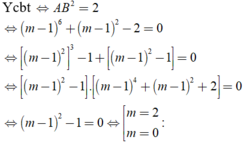
Chọn B.
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị A , B sao cho đường thẳng AB vuông góc với đường thẳng : y = x + 2 .
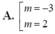

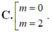
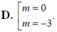
Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
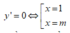
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
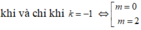
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị là A và B sao cho đường thẳng AB vuông góc với đường thẳng d : y = x + 2 Số phần tử của S là
A. 0
B. 1
C. 2
D. 3
Tìm tất cả các giá trị thực của tham số m để điểm M( 2m3; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y= 2x3-3( 2m+ 1) x2+ 6m( m+1) x+1 (C) một tam giác có diện tích nhỏ nhất.
A. -1
B. 0
C. 1
D. 2
+ Ta có: y’ = 6x2-6( 2m+1) x+ 6m(m+1)
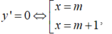
do đó hàm số luôn có cực đại cực tiểu với mọi m.
+ Tọa độ các điểm CĐ, CT của đồ thị là A( m; 2m3+3m2+1 ) và B( m+1; 2m3+3m2)
Suy ra AB = √2 và phương trình đường thẳng AB: x+ y-2m3-3m2-m-1=0.
+ Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
d ( M , A B ) = 3 m 2 + 1 2 ⇒ d ( M , A B ) ≥ 1 2 ⇒ m i n d ( M , A B ) = 1 2
đạt được khi m=0
Chọn B
Tìm tất cả các giá trị thực của tham số m để điểm M ( 2 m 3 ; m ) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 một tam giác có diện tích nhỏ nhất
A. m = 2
B. m = 0
C. m = 1
D. m = -1
Chọn B
Ta có:
![]()
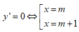
⇒ ∀ m ∈ ℝ , hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
![]()
Suy ra A B = 2
và phương trình đường thẳng x + y - 2 m 3 - 3 m 2 - m - 1 = 0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
Ta có:
![]()
![]()
⇒ đạt được khi m = 0
Tìm tổng tất cả các giá trị thực của tham số m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = 2 x 3 + 3 ( m - 1 ) x 2 + 6 m ( 1 - 2 m ) x song song đường thẳng y= -4x.
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để điểm M 2 m 3 ; m cùng với hai điểm cực trị của đồ thị hàm số y = 2 x 3 - 3 2 m + 1 x 2 + 6 m m + 1 x = 1 tạo thành một tam giác có diện tích nhỏ nhất.
A. m = 2
B. m = 0
C. m = 1
D. m = -1
Tìm các giá trị của tham số m để đồ thị hàm số y = 2 x 3 + 3 ( m - 3 ) x 2 + 11 - 3 m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C(0;-1) thẳng hàng
A. m = 4
B. m = 1
C. m = -3
D. m = 2
Chọn A
Phương pháp tự luận]
y ' = 6 x 2 + 6 ( m - 3 ) x
![]()
Hàm số có 2 cực trị ⇔ m ≠ 3
Khi đó đồ thị hàm số đã cho có 2 điểm cực trị A(0;11-3m)
![]()
![]()
Phương trình đt AB: ( 3 - m ) 2 x + y - 11 + 3 m = 0
![]()
![]()
Tìm các giá trị của tham số m để đồ thị hàm số y= 2x3+ 3( m-3) x2+ 11- 3m có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C( 0; -1) thẳng hàng
A. -2
B. -3
C. 3
D. 4
Ta có đạo hàm y’ = 6x2+ 6( m-3) x
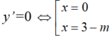
Hàm số có 2 cực trị khi 3-m≠0 hay m≠3
Khi đó đồ thị hàm số đã cho có 2 điểm cực trị A( 0; 11-3m) và B( 3-m; m3-9m2+ 24m -16) ; A B → = ( 3 - m , ( 3 - m ) 3 ) .
Phương trình đt AB: ( 3-m) 2x+ y-11+3m=0
Để 3 điểm A; B; C hẳng hàng khi và chỉ khi C thuộc đường thẳng AB.
Hay : -1-11=3m= 0 hay m= 4.
Chọn D.