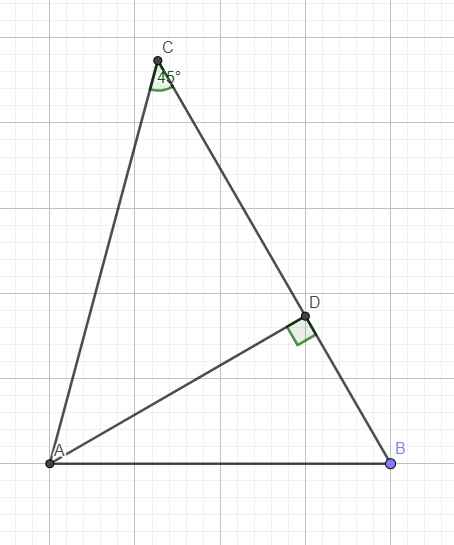
cho tam giác có góc C = 45 độ . AB nhân AC = 32 căn 6; AB chia AC = căn 6 chia 3 . tính số đo cạnh BC; góc B và diện tích tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC có góc C bằng 45 độ, AB. AC=32\(\sqrt{6}\), AB:AC=\(\sqrt{6}\):3. Tính BC, góc B và diện tích tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)
Đúng 0
Bình luận (0)
1) Cho tam giác ABC không vuông có BC= 3 cộng căn 3, góc C=60 độ, góc B=45 độ.Tính chiều cao AH và chu vi tam giác ABC.
2) Cho tam giác ABC không vuông có góc A=105 độ, góc B=45 độ,BC=4cm.TÍnh AB,AC
3) Cho tam giác ABC có góc A=60 độ, AB=28cm,AC=35cm.Kẻ Bh vuông góc với AC. Tính BH,BC.
giải giúp mình vs, 1 câu cx đc (^_^)
\(\left[{}\begin{matrix}\\\\\\\end{matrix}\right.\prod\limits^{ }_{ }\int_{ }^{ }dx\sinh_{ }^{ }⋮\begin{matrix}&&&\\&&&\\&&&\\&&&\\&&&\\&&&\end{matrix}\right.\Cap\begin{matrix}&&\\&&\\&&\\&&\\&&\\&&\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B bằng 45 độ, AB=căn 18 (cm), BC=7 (cm). Tính AC.
Bài 6: Cho tam giác ABC. Vẽ AH vuông góc với BC tại H. Biết AH = 3, AB = 5 , AC = căn bậc của 45 . Tính độ dài cạnh BC
\(BH=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(CH=\sqrt{45-3^2}=6\left(cm\right)\)
=>BH+CH=BC=10(cm)
Đúng 2
Bình luận (0)
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=4cm\)
Theo định lí Pytago tam giác AHC vuông tại H
\(CH=\sqrt{AC^2-AH^2}=6cm\)
-> BC = BH + CH = 4 + 6 = 10 cm
Đúng 1
Bình luận (0)
tam giác ABC có AB=AC VÀ C = 45 ĐỘ
a, tính các góc căn lại của tam giác ABC
b, hỏi tam giác ABC có là tam giác cân đều vuông vuông cân k
Cho tam giác ABC có C=45 độ. AB.AC =\(32\sqrt{6}\), \(\frac{AB}{AC}=\frac{\sqrt{6}}{3}\)
a) Tính các cạnh vào góc còn lại của tam giác ABC
b) Tính \(S_{ABC}\)
Cho tam giác ABC có góc C = 450, AB*AC=\(32\sqrt{6}\), \(\frac{AB}{AC}=\frac{\sqrt{6}}{3}\). Tính số đo cạnh BC, góc B và SABC
Cho tam giác ABC có góc C = 450, AB*AC=\(32\sqrt{6}\), \(\frac{AB}{AC}=\frac{\sqrt{6}}{3}\). Tính số đo cạnh BC, góc B và SABC
Cho tam giác ABC có góc C = 450, AB*AC=\(32\sqrt{6}\), \(\frac{AB}{AC}=\frac{\sqrt{6}}{3}\). Tính số đo cạnh BC, góc B và SABC
Đặt AB = x>0 , AC = y>0 , BC = z>0
Theo đề bài , ta có : \(\begin{cases}xy=32\sqrt{6}\\\frac{x}{y}=\frac{\sqrt{6}}{3}\end{cases}\) \(\Leftrightarrow\begin{cases}x=8\\y=4\sqrt{6}\end{cases}\)Theo định lí Cosin, ta có : \(x^2=y^2+z^2-2yz.cos45^o\Leftrightarrow64=96+z^2-8\sqrt{3}z\)\(\Leftrightarrow\left[\begin{array}{nghiempt}z=4+4\sqrt{3}\\z=-4+4\sqrt{3}\end{array}\right.\)
Vậy BC = \(4+4\sqrt{3}\) hoặc BC = \(4\sqrt{3}-4\)
Theo định lí Cosin, ta có : \(y^2=x^2+z^2-2xz.cosB\Rightarrow cosB=\frac{x^2+z^2-y^2}{2xz}\)+Với \(\begin{cases}x=8\\y=4\sqrt{6}\\z=4+4\sqrt{3}\end{cases}\) thì \(cosB=\frac{1}{2}\Rightarrow\widehat{B}=60^o\)
+Với \(\begin{cases}x=8\\y=4\sqrt{6}\\z=4\sqrt{3}-4\end{cases}\) thì \(cosB=-\frac{1}{2}\Rightarrow\widehat{B}=120^o\)
Để tính diện tích tam giác ABC, ta áp dụng công thức \(S_{\Delta ABC}=\frac{1}{2}BC.AC.sinC\)Chứng minh như sau : Kẻ đường cao AK (K thuộc BC)
Trong tam giác vuông AKC có : \(AK=sinC.AC\)
Ta có : \(S_{\Delta ABC}=\frac{1}{2}BC.AK=\frac{1}{2}BC.AC.SinC\)
+Với \(\begin{cases}x=8\\y=4\sqrt{6}\\z=4+4\sqrt{3}\end{cases}\) thì \(S_{\Delta ABC}=\frac{1}{2}AC.BC.sin45^o=\frac{1}{2\sqrt{2}}.4\sqrt{6}.\left(4+4\sqrt{3}\right)=24+8\sqrt{3}\)
+Với \(\begin{cases}x=8\\y=4\sqrt{6}\\z=4\sqrt{3}-4\end{cases}\) thì \(S_{\Delta ABC}=\frac{1}{2}AC.BC.sin45^o=\frac{1}{2\sqrt{2}}.4\sqrt{6}.\left(-4+4\sqrt{3}\right)=24-8\sqrt{3}\)
Đúng 0
Bình luận (0)