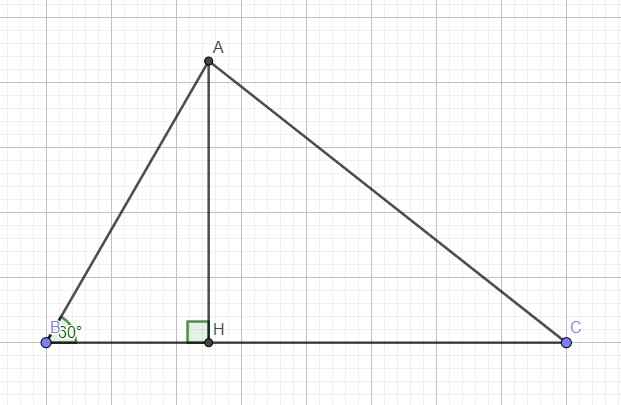
Cho tam giác ABC, B = 60 độ, BC = 8cm; AB + AC = 12cm. Tính độ dài cạnh AB

Những câu hỏi liên quan
Cho tam giác ABC , góc B = 60 độ, BC = 8cm; AB + AC = 12cm . Tính độ dài cạnh AB.
Cho tam giác ABC , góc B = 60 độ, BC = 8cm; AB + AC = 12cm . Tính độ dài cạnh AB.
Cho tam giác ABC vuông tại A . Biết B=60 độ, BC=8cm. Tính độ dài AC
Cho tam giác ABC có góc B = 60 độ , BC =8cm, AB + AC =12cm. Tính độ dài AB
Dựng AH vuông góc với BC, đặt AB = x, ta có : AH = x.sin B = x.sin60 = x.căn 3 / 2
HB = x.cos 60 = x/2 => HC = BC - HB = 8 - x/2 = (16 - x)/2
AC = 12 - AB = 12 - x
Trong tam giác vuông AHC : AH^2 + HC^2 = AC^2
hay (x. căn 3 /2)^2 + (16 - x)^2/4 = (12 - x)^2
<=> 3x^2 + (16 - x)^2 = 4(12 - x)^2
Giải phương trình này tìm được x = 5
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B = 60 độ BC=8cm AB+AC=12cm . Tính độ dài AB
giải chi tiết hộ mình với ạ!!!
Dựng AH vuông góc với BC, đặt AB = x, ta có : AH = x.sin B = x.sin60 = x.căn 3 / 2 HB = x.cos 60 = x/2 => HC = BC - HB = 8 - x/2 = (16 - x)/2
AC = 12 - AB = 12 - x
Trong tam giác vuông AHC : AH^2 + HC^2 = AC^2
hay (x. căn 3 /2)^2 + (16 - x)^2/4 = (12 - x)^2
<=> 3x^2 + (16 - x)^2 = 4(12 - x)^2
Giải phương trình này tìm được x = 5
Vậy AB = 5cm
AC = 12 - AB = 12 - x
Trong tam giác vuông AHC : AH^2 + HC^2 = AC^2
hay (x. căn 3 /2)^2 + (16 - x)^2/4 = (12 - x)^2
<=> 3x^2 + (16 - x)^2 = 4(12 - x)^2
Giải phương trình này tìm được x = 5
Vậy AB = 5cm
Đúng 1
Bình luận (7)
Cho tam giác ABC có góc B = 60 độ, BC = 8cm, AB + AC = 12cm. Tính AB, AC
(ko dùng sin,cos)
Kẻ đường cao AH ứng với BC
Đặt \(AB=x\) với \(0< x< 12\Rightarrow AC=12-x\)
Đặt \(BH=y\Rightarrow CH=8-y\) (với \(0< y< 8\))
Trong tam giác vuông ABH ta có:
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=\dfrac{x}{2}\Rightarrow y=\dfrac{x}{2}\)
\(\Rightarrow CH=8-y=8-\dfrac{x}{2}\)
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=\dfrac{x\sqrt{3}}{2}\)
Áp dụng Pitago cho tam giác vuông ACH:
\(AC^2=AH^2+CH^2\Leftrightarrow\left(12-x\right)^2=\left(\dfrac{x\sqrt{3}}{2}\right)^2+\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\Rightarrow x=5\)
\(\Rightarrow AC=12-x=7\)
Vậy \(AB=5cm,AC=7cm\)
Đúng 0
Bình luận (2)
Cho tam giác ABC có AB=6cm có góc B=60 độ, BC=8cm, AB+AC=12cm. TÍnh các độ dài AB,AC
Tam giác ABC vuông tại A, B=60.
⇒ Tam giác ABC là 1 nửa tam giác đều
⇒AB = \(\frac{BC}{2}\) =4cm.
AC=12‐4=8cm
Vậy AB=4cm
AC=8cm
Đúng 0
Bình luận (2)
Kẻ: \(AH\perp BC\).Đặt \(AB=2x\Rightarrow BH=x\Rightarrow AH=x\sqrt{3};HC=8-x\)
Áp dụng định lí Pi-ta-go có:
\(AC=\sqrt{\left(x\sqrt{3}\right)^2+\left(8-x\right)^2}=\sqrt{4x^2-16x+64}\)
Do \(AB+AC=12\Rightarrow2x+\sqrt{4x^2-16x+64}=12\)
Giải phương trình có x = 2,5
\(\Rightarrow AB=2x=2.2,5=5cm\)
Thay số vào tính được AC =))
Đúng 1
Bình luận (0)
tam giác ABC có B + C = 60 độ , AB = 8cm . Số đo cạnh AC là ??
tam giác ABC có A = 120 ĐỘ ,AB = AC ,BC = 12CM .Độ dài đường cao AH là ???
cho tam giác ABC có AB=8cm, AC=12cm, góc A = 60 độ. Tính BC.
Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(8^2+12^2-BC^2=2\cdot8\cdot12\cdot\dfrac{1}{2}\)
=>\(BC^2=64+144-96=64+48=112\)
=>\(BC=4\sqrt{7}\left(cm\right)\)
Đúng 2
Bình luận (0)