Cho tam giác ABC có đỉnh B(-1;3), trung tuyến AM có phương trình 3x+2y-9=0: trung tuyến CN: x-1=0
a) Viết pt tổng quát đường trung tuyến BE
b) Tìm tọa độ các đỉnh AC
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Tham khảo:
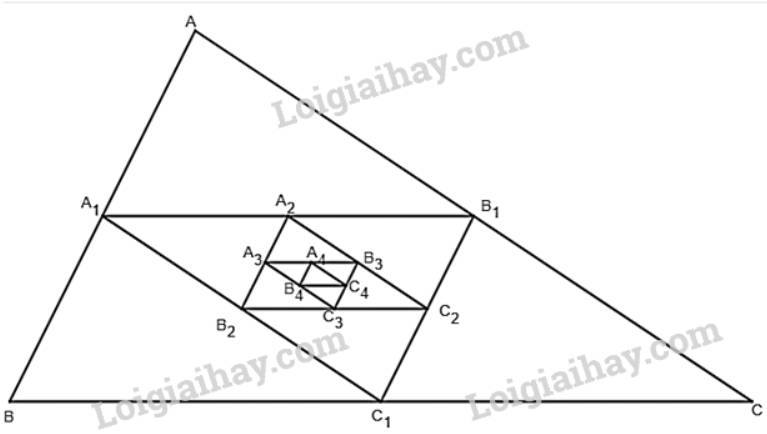
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
1.Cho tam giác ABC cân đỉnh A, góc BAx là góc ngoài tại đỉnh A của tam giác ABC. Chứng minh rằng góc BAx bằng 2.B
2.Cho tam giác ABC có góc A bằng 90, góc B bằng 60. Chứng minh rằng AB = 1/2 BC.
Cho tam giác ABC có đỉnh A(1; 1), B(-2; 4) và G(1; 2) là trọng tâm của tam giác. Khi đó tọa độ đỉnh C là:
A. C(0; 7/3)
B. C(4; 1)
C. C(2; -3)
D. C(-2; 2)
Cho tam giác ABC có A(1;-1); B(-1;0); C(3;3). Độ dài đường cao xuất phát từ đỉnh A của tam giác ABC bằng
A. 2
B. 3
C. 5
D. 6
Đáp án: A
Ta có: 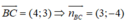
Đường thẳng BC đi qua B và có vecto 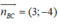 là vecto pháp tuyến:
là vecto pháp tuyến:
BC: 3(x + 1) - 4(y - 0) = 0 ⇔ 3x - 4y + 3 = 0
Gọi AH là đường cao của tam giác ABC
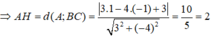
cho tam giác ABC có góc A=75 độ 1 đường thẳng đi qua đỉnh A và cắt BC tại M và chia tam giác ABC thành 2 tam giác cân .Tính góc B và C của tam giác ABC
Cho tam giác ABC có CosB=1/3 , AC=b đường cao hạ từ đỉnh B bằng tổng hai đường cao còn lại . Tính diện tích của tam giác ABC
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;-3), phương trình đường phân giác trong đỉnh B là x+y-2=0 và phương trình đường trung tuyến hạ từ đỉnh C là x+8y-7=0. Tìm tọa độ các đỉnh B và C của tam giác ABC
goi B(a; b) N( c; d)
\(N\in\left(CN\right)\Rightarrow\)c+8d-7 = 0(1)
N la trung diem AB\(\Rightarrow2c=1+a\left(2\right)\)
2d = -3 +b (3)
B\(\in\left(BM\right)\)\(\Rightarrow\)a+b -2 =0 (4)
tu (1) (2) (3) (4) \(\Rightarrow a=-5;b=7\Rightarrow B\left(-5;7\right)\)
dt (AE) qua vuong goc BM. \(\Rightarrow pt\)(AE):x-y-4 = 0
tọa độ H \(\left\{{}\begin{matrix}x-y-4=0\\x+y-2=0\end{matrix}\right.\Rightarrow H\left(3;-1\right)\);H là trung điểm AE
\(\Rightarrow E\left(5;1\right)\). vì ptdt (BE) cung la ptdt qua (BC):
3x+5y-20 =0
tọa độ C là nghiệm hệ \(\left\{{}\begin{matrix}3x+5y-20=0\\x+8y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{139}{21}\\\dfrac{1}{21}\end{matrix}\right.\)
\(\Rightarrow C\left(\dfrac{139}{21};\dfrac{1}{21}\right)\)
Cho tam giác ABC có các đỉnh A(-1;3), B(1;0) và C(2;-1). Tính độ dài đường cao của tam giác ABC vẽ từ điểm A?
A. 1
B. 2 2
C. 2
D. 3 2 2
Đáp án: B
Ta có A(-1;3), B(1;0) và C(2;-1)
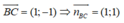
Phương trình đường thẳng BC có dạng: (x - 1) + (y - 0) = 0 ⇔ x + y - 1 = 0
Độ dài đường cao của tam giác ABC kẻ từ điểm C chính bằng khoảng cách từ điểm A đến đường thẳng BC:
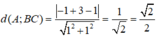
Cho tam giác ABC có góc A = 100 độ, góc B=50 độ. Tia phân giác trong tại đỉnh B cắt
tia phân giác ngoài tại đỉnh C của tam giác ABC ở O
Tính góc BOC và góc AOB
Cho tam giác ABC có A(-1; 1); trực tâm H(-31; 41) và tâm đường tròn ngoại tiếp tam giác ABC là I(16; 18). Tìm tọa độ các đỉnh B; C