Cho hàm số y=f(x) có đạo hàm dương trên [1;2] thỏa mãn f ( 1 ) = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f(2)
A. f ( 2 ) = 1 e 2
B. f ( 2 ) = 2 e 2
C. f ( 2 ) = 4 e 2
D. f ( 2 ) = 8 e 2
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 4 ( x 2 + m x + 9 ) với mọi. Có bao nhiêu giá trị nguyên dương của m để hàm số g(x) = f(3 - x) đồng biến trên khoảng 3 ; + ∞
A. 5
B. 6
C. 7
D. Vô số
Cho hàm số y = f x có đạo hàm dương trên 1 ; 2 thỏa mãn f 1 = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f 2 .
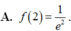
![]()
![]()
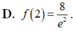
Cho hàm số y = f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như hình bên. Hàm số y = log x f 2 x đồng biến trên khoảng

A. (1;2)
B. - ∞ ; - 1
C. (-1;0)
D. (-1;1)
Cho hàm số y=f(x) liên tục, nhận giá trị dương trên R và có bảng xét dấu đạo hàm như dưới đây

Hàm số y = log 2 f 2 x đồng biến trên khoảng
A. (1;2)
B. - ∞ ; - 1
C. (-1;0)
D. (-1;1)
Đặt g ( x ) = log 2 ( f ( 2 x ) ) ,
ta có g ' ( x ) = 2 f ' ( 2 x ) f ( 2 x ) ln 2
Theo giả thiết, ta có f ( 2 x ) > 0 , ∀ x ∈ ℝ
Do đó
g ' ( x ) ≥ 0 ⇔ f ' ( 2 x ) ≥ 0 ⇔ [ - 1 ≤ 2 x ≤ 1 2 x ≥ 2 ⇔ [ - 1 2 ≤ x ≤ 1 2 x ≥ 1
(dấu bằng xảy ra tại hữu hạn điểm). Suy ra hàm số y=g(x) đồng biến trên các khoảng - 1 2 ; 1 2 và 1 ; + ∞ . Chọn A.
Chọn đáp án A.
Cho hàm số y = f(x) đạo hàm f’(x) = –x2 – 1. Với các số thực dương a, b thỏa mãn a<b. Giá trị nhỏ nhất của hàm số f(x) trên đoạn [a;b] bằng
A. f(b)
B. f( a b )
C. f(a)
D. f( a + b 2 )
Đáp án A
Phương pháp giải:
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Lời giải:
Ta có ![]() suy ra f(x) là hàm số nghịch biến trên [a;b]
suy ra f(x) là hàm số nghịch biến trên [a;b]
Mà ![]() . Vậy
. Vậy ![]()
Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
A. f(a)
B. f a b
C. f( b)
D. f a + b 2
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy m i n [ a ; b ] f ( x ) = f ( b )
Chọn C.
Cho hàm số f(x) luôn dương và có đạo hàm liên tục trên đoạn [1;4]. Biết rằng f ' ( x ) = e x f ( x ) , ∀ x∈ [1;4] và f(1)=1. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f' (x)=1, trục hoành và hai đường thẳng x=1,x=4.
A. e e 2 + 1 .
B. e 2 e 2 + 1 .
C. e 2 e 2 + 2 .
D. e e 2 + 2 .
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng

A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)