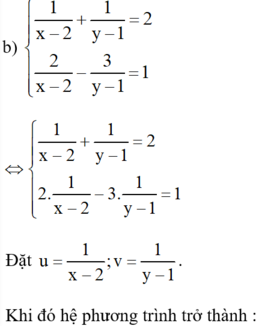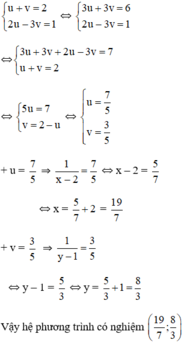22x+3y=1; 12x-7y=-9 thì trung bình cộng của x và y bằng

Những câu hỏi liên quan
Nếu 22x+3y=1 và 12x-7y=-9 thì trung bình cộng của x và y sẽ là
Ta có:
\(\hept{\begin{cases}22x+3y=1\\12x-7y=-9\end{cases}\Rightarrow\left(22x+3y\right)-\left(12x-7y\right)=10\Rightarrow10x+10y=10}\)
=> x+y=1 =>TBC x+y là \(\frac{1}{2}\)
Đúng 0
Bình luận (0)
Phần tự luận
Nôi dung câu hỏi 1
Giải các hệ phương trình sau
a) x + y = 2 2 x - 3 y = 9
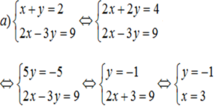
Vậy hệ phương trình có nghiệm duy nhất là (x; y) = (3; -1)
Đúng 0
Bình luận (0)
Cho hệ phương trình
x
+
1
y
2
2
x
−
3
y
1
. Biết nghiệm của hệ phư...
Đọc tiếp
Cho hệ phương trình x + 1 y = 2 2 x − 3 y = 1 . Biết nghiệm của hệ phương trình là (x; y), tính 5 x y
A. 35 3
B. 21 5
C. 7 3
D. 21 25
ĐK: y ≠ 0
Ta có
x + 1 y = 2 2 x − 3 y = 1 ⇔ 2 x + 2 y = 4 2 x − 3 y = 1 ⇔ x + 1 y = 2 5 y = 3 ⇔ y = 5 3 x + 1 5 3 = 2 ⇔ x = 7 5 y = 5 3
Vậy hệ phương trình có 1 nghiệm duy nhất ( x ; y ) = 7 5 ; 5 3 ⇒ 5 x y = 21 5
Đáp án: B
Đúng 0
Bình luận (0)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
1
x
-
2
+
1
y
-
1...
Đọc tiếp
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải: 1 x - 2 + 1 y - 1 = 2 2 x - 2 - 3 y - 1 = 1
Giải hệ phương trình:
\(\left\{{}\begin{matrix}y^3+3y^2+y-22x+21=\left(2x+1\right)\sqrt{2x-1}\\2x^2-11x+9=2y\end{matrix}\right.\)
22x+22x+1+22x+2+...+22x+1918=21923-24
Đặt \(A=2^{2x}+2^{2x+1}+...+2^{2x+1918}\)
=>\(2\cdot A=2^{2x+1}+2^{2x+2}+...+2^{2x+1919}\)
=>\(A=2^{2x+1919}-2^{2x}\)
Theo đề, ta có; \(2^{2x+1919}-2^{2x}=2^{1923}-2^4\)
=>\(2^{2x}\cdot\left(2^{2019}-1\right)=2^4\left(2^{2019}-1\right)\)
=>2x=4
=>x=2
Đúng 0
Bình luận (0)
GIẢI GIÙM MÌNH HỆ GỒM HAI PT NÀY VỚI
\(y^3+3y^2+y+4x^2-22x+21=\left(2x+1\right)\sqrt{2x-1}\)
\(2x^2-11x+9=2y\)
giải hệ phương trình \(\hept{\begin{cases}\sqrt{x-3y}-\sqrt{5x-y}=0\\15\sqrt{5x-y}+22x+4y=15\end{cases}}\)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
a)
1
x
−
1
y
1...
Đọc tiếp
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
a) 1 x − 1 y = 1 3 x + 4 y = 5 Đặt u = 1 x ; v = 1 y b) 1 x − 2 + 1 y − 1 = 2 2 x − 2 − 3 y − 1 = 1 đặt u = 1 x − 2 ; v = 1 y − 1
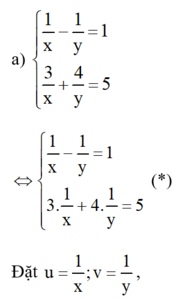
hệ phương trình (*) trở thành :
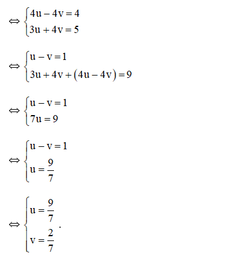
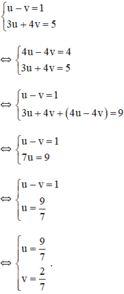
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
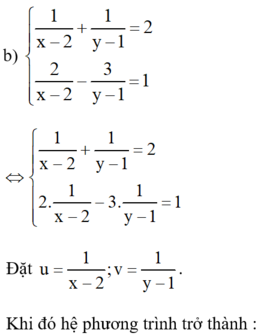
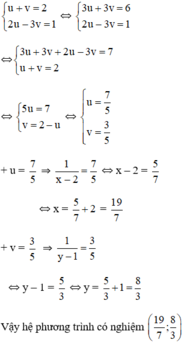
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
Đúng 0
Bình luận (0)