Cho hàm số y=kx có đồ thị đi qua điểm A(1;-4)
a) Tìm k và vẽ đồ thị hàm số trên.
b) Trong các điểm sau, điểm nào thuộc đồ thị hàm số trên? Vì sao?
M(-1;-4); N(5;-20); P(-3;12)
c) Tìm x khi y=8, y=-4/5, y=1/4

Những câu hỏi liên quan
Cho hàm số y=kx có đồ thị đi qua điểm A(1;-4)
a) Tìm k và vẽ đồ thị hàm số trên.
b) Trong các điểm sau, điểm nào thuộc đồ thị hàm số trên? Vì sao?
M(-1;-4); N(5;-20); P(-3;12)
c) Tìm x khi y=8, y=-4/5, y=1/4
a: Thay x=1 và y=-4 vào (d), ta được:
k=-4
Đúng 0
Bình luận (0)
Cho hàm số y=kx có đồ thị đi qua điểm A(1;-4)
a) Tìm k và vẽ đồ thị hàm số trên.
b) Trong các điểm sau, điểm nào thuộc đồ thị hàm số trên? Vì sao?
M(-1;-4); N(5;-20); P(-3;12)
c) Tìm x khi y=8, y=-4/5, y= 1/4
a: Thay x=1 và y=-4 vào (d), ta được:
1xk=-4
hay k=-4
Đúng 2
Bình luận (0)
a.k=(-4)
b.Điểm N thuộc đths vì (-4).5=(-20)
P thuộc đths vì (-3).(-4)=12
c.Khi y=8 thì x=(-2)
Khi y=\(-\dfrac{4}{5}\)thì x=\(\dfrac{1}{5}\)
Khi y=\(\dfrac{1}{4}\)thì x=\(-\dfrac{1}{16}\)
Đúng 1
Bình luận (0)
\(a,x=1;y=-4\Rightarrow k=-4\\ b,\text{Thay }x=-1;y=-4\Rightarrow\left(-1\right)\left(-4\right)=-4\left(sai\right)\\ \text{Thay }x=5;y=-20\Rightarrow5\left(-4\right)=-20\left(đúng\right)\\ \text{Thay }x=-3;y=12\Rightarrow\left(-3\right)\left(-4\right)=12\left(đúng\right)\\ \text{Vậy }M\notin y=-4x;N,P\in y=-4x\\ c,y=-4x\Rightarrow x=\dfrac{y}{-4}\\ y=8\Rightarrow x=\dfrac{8}{-4}=-2\\ y=-\dfrac{4}{5}\Rightarrow x=\dfrac{-\dfrac{4}{5}}{-4}=\dfrac{1}{5}\\ y=\dfrac{1}{4}\Rightarrow x=\dfrac{\dfrac{1}{4}}{-4}=-\dfrac{1}{16}\)
Đúng 2
Bình luận (0)
điểm M(4;5;9) thuộc đồ thị hàm số y=kx.
Đồ thị hàm số trên đi qua điểm..........
Sao điểm M trên mặt phẳng tọa độ Oxy mà tọa độ lại là $M(4;5;9)$ hả bạn?
Đúng 0
Bình luận (0)
cho hàm số y = kx ( k là hệ số khác 0 ) có đồ thị là đường thẳng đi qua M ( -1, 2 )
a ) tìm k và vẽ đồ thị hàm số trên
b) chứng minh ba điểm O ,M và A ( 2,-4 ) thẳng hàng
Cho hàm số y = kx + 1 ,trong đó k là tham số .Tìm k để tìm đồ thị hàm số đi qua điểm A( 1; 4) với giá trị K vừa tìm được hàm số đồng biến hay nghịch biến
Thay x=1 và y=4 vào y=kx+1, ta được:
k+1=4
=>k=3
=>y=3x+1
=>Hàm số đồng biến
Đúng 0
Bình luận (0)
Cho hàm số: y
x
3
− (m + 4)
x
2
− 4x + m (1)a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m 0d) Xác định k để (C) cắt đường thẳng y kx tại ba điểm phân biệt.
Đọc tiếp
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
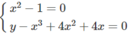
Giải hệ, ta được hai nghiệm:
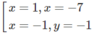
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
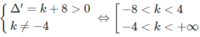
Đúng 0
Bình luận (0)
Xác định giá trị m, k biết:
a. Đồ thị hàm số \(y=3x+m\)đi qua điểm (2; 7).
b Đồ thị hàm số \(y=kx+5\)đi qua điểm (2;11).
Do đồ thị hàm số đi qua điểm ( 2;7 )
\(\Rightarrow x=2;y=7\)
Thay vào hàm số \(y=3x+m\) ta được :
\(\Rightarrow7=3.2+m\)
\(\Rightarrow m=1\)
b, do đồ thị hàm số đi qua điểm ( 2 ; 11 )
\(\Rightarrow x=2;y=11\)
Thay vào hàm số \(y=kx+5\) ta được :
\(11=2k+5\)
\(\Rightarrow k=3\)
k mk nha
Đúng 0
Bình luận (0)
Cho hàm số y=kx
a) Tìm k biết đồ thị hàm số đi qua điểm M\(\left(\frac{5}{2};-5\right)\)
b) Vẽ đồ thị với k vừa tìm được
c) CT O, A(1; -2) và B(2; 1) không thẳng hàng
Lâu rồi mới chơi dạng này, ko biết có đúng ko nx!
a) Thay x = 5/2 ; y = -5 ta được \(-5=k.\frac{5}{2}\Rightarrow k=\left(-5\right):\frac{5}{2}=-2\)
Vậy ta có hàm số \(y=-2x\)
b) Với x = 1 suy ra y = -2. Ta có toạ độ D(1;-2)
c) Quên mất cách làm rồi, mà cho hỏi CT O là cái gì vại? Để biết đường còn suy nghĩ với lục lọi sách giáo khoa tìm hướng giải, you viết tắt quá ai hiểu nổi @@
Đúng 0
Bình luận (2)
Tìm hàm số y=kx + b biết rằng đồ thị đó đi qua các điểm
A(8;-1) và B(√2; -1)




















